【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,常数
为自然对数的底数,常数![]() .
.
(1)求函数![]() 在区间
在区间![]() 上的零点个数;
上的零点个数;
(2)函数![]() 的导数
的导数![]() ,是否存在无数个
,是否存在无数个![]() ,使得
,使得![]() 为函数
为函数![]() 的极大值点?说明理由.
的极大值点?说明理由.
参考答案:
【答案】(1)1(2)存在
【解析】【试题分析】(1)对函数求导后得到函数的单调区间,利用二分法判断函数在给定区间上只有一个零点.(2)原命题等价于,存在无数个![]() ,使得
,使得![]() 成立,求得
成立,求得![]() 的表达式,构造为函数
的表达式,构造为函数![]() ,利用导数证得
,利用导数证得![]() 存在负值即可.
存在负值即可.
【试题解析】
(1)![]() ,当
,当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增;
单调递增;
因为![]() ,所以存在
,所以存在![]() ,使
,使![]() ,
,
且当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
故函数![]() 在区间
在区间![]() 上有1个零点,即
上有1个零点,即![]() .
.
(2)(法一)当![]() 时,
时, ![]() .
.
因为当![]() 时,
时, ![]() ;当
;当![]() ,
, ![]() .
.
由(1)知,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
下证:当![]() 时,
时, ![]() ,即证
,即证![]() .
.
![]() ,
,
记![]() …
…
![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
由![]() ,
,
所以存在唯一零点![]() ,使得
,使得![]() ,且
,且![]() 时,
时, ![]() 单调递减,
单调递减,
![]() 时,
时, ![]() 单调递增.
单调递增.
所以当![]() 时,
时, ![]() .……
.……
由![]() ,得当
,得当![]() 时,
时, ![]() .
.
故![]() .
.
当![]() 时,
时, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 单调递减.
单调递减.
所以存在![]() ,使得
,使得![]() 为
为![]() 的极大值点.
的极大值点.
(2)(法二)因为当![]() 时,
时, ![]() ;当
;当![]() ,
, ![]() .
.
由(1)知,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以存在无数个![]() ,使得
,使得![]() 为函数
为函数![]() 的极大值点,即存在无数个
的极大值点,即存在无数个![]() ,使得
,使得![]() 成立, ①…由(1),问题①等价于,存在无数个
成立, ①…由(1),问题①等价于,存在无数个![]() ,使得
,使得![]() 成立,
成立,
因为![]() ,
,
记![]() …
…
![]() 因为
因为![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 单调递增,因为
单调递增,因为![]() ,
,
所以存在唯一零点![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增;
单调递增;
所以,当![]() 时,
时, ![]() , ②…
, ②…
由![]() ,可得
,可得![]() ,代入②式可得
,代入②式可得![]() ,
,
当![]() 时,
时, ![]() ,
,
所以,必存在![]() ,使得
,使得![]() ,即对任意
,即对任意![]() 有解,
有解,
所以对任意![]() ,函数
,函数![]() 存在极大值点为
存在极大值点为![]() .…
.…
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆的中心为原点O,长轴在x轴上,离心率
 ,过左焦点F1作x轴的垂线交椭圆于A,
,过左焦点F1作x轴的垂线交椭圆于A, 两点
两点 .
.(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P,
 ,过P、
,过P、 作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若
作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若 ,求圆Q的标准方程.
,求圆Q的标准方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
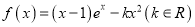 .
.(Ⅰ)当
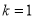 时,求函数
时,求函数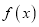 的单调区间;
的单调区间;(Ⅱ)当
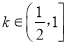 时,求函数
时,求函数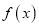 在
在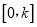 上的最大值M.
上的最大值M. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018广东省深中、华附、省实、广雅四校联考】已知椭圆
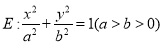 的离心率为
的离心率为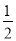 ,圆
,圆 与
与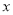 轴交于点
轴交于点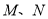 ,
, 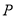 为椭圆
为椭圆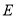 上的动点,
上的动点,  ,
, 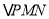 面积最大值为
面积最大值为 .
.(I)求圆
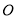 与椭圆
与椭圆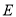 的方程;
的方程;(II)圆
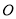 的切线
的切线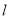 交椭圆于点
交椭圆于点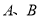 ,求
,求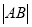 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
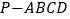 ,底面
,底面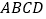 为菱形,
为菱形,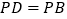 ,
,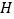 为
为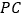 上的点,过
上的点,过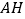 的平面分别交
的平面分别交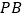 ,
, 于点
于点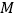 ,
,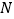 ,且
,且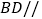 平面
平面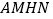 .
.(1)证明:
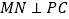 ;
;(2)当
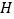 为
为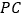 的中点,
的中点,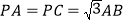 ,
,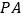 与平面
与平面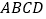 所成的角为
所成的角为 ,求二面角
,求二面角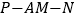 的余弦值.
的余弦值.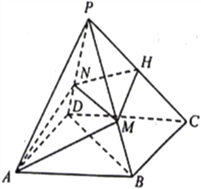
-
科目: 来源: 题型:
查看答案和解析>>【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
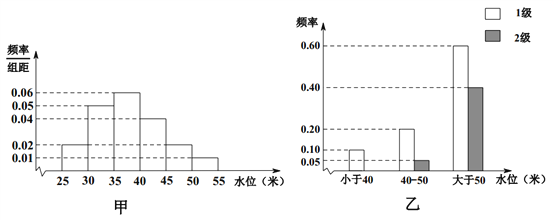
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案
防控等级
费用(单位:万元)
方案一
无措施
0
方案二
防控1级灾害
40
方案三
防控2级灾害
100
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村计划建造一个室内面积为800m2的矩形蔬菜温室,在室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
相关试题

