【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)探究函数![]() 的极值点情况,并说明理由.
的极值点情况,并说明理由.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)先求函数导数,根据导数几何意义得切线斜率,再根据点斜式写出切线方程(2)先求导数,转化研究函数![]() ,利用导数易得
,利用导数易得![]() 先减后增,讨论与两个端点值以及最小值点大小关系,确定极值点情况.
先减后增,讨论与两个端点值以及最小值点大小关系,确定极值点情况.
试题解析:解:(Ⅰ)依题意![]() ,故
,故![]() ,
,
因为![]() ,故所求切线方程为
,故所求切线方程为![]() ,即
,即![]() .
.
(Ⅱ)![]() ,
,![]() ,
,
记![]() ,则
,则![]()
![]() ,
,![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() 取得极小值
取得极小值![]() ,
,
又![]() ,
,![]() ,
,![]() .
.
(i)当![]() ,即
,即![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 在区间
在区间![]() 上无极值点;
上无极值点;
(ii)当![]() ,即
,即![]() 时,
时,![]() 有两不同解,函数
有两不同解,函数![]() 在
在![]() 上有两个极值点;
上有两个极值点;
(iii)当![]() ,即
,即![]() 时,
时,![]() 有一解,函数
有一解,函数![]() 在区间
在区间![]() 上有一个极值点;
上有一个极值点;
(iv)当![]() ,即
,即![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上无极值点.
上无极值点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)当曲线
 在点
在点 处的切线与直线
处的切线与直线 垂直时,求
垂直时,求 的值;
的值;(2)若函数
 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 x2+lnx.
x2+lnx.
(1)求函数f(x)的单调区间;
(2)求证:当x>1时, x2+lnx<
x2+lnx<  x3 .
x3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)讨论函数
 的单调性;
的单调性;(Ⅱ)已知点
 ,曲线
,曲线 在点
在点
 处的切线
处的切线 与直线
与直线 交于点
交于点 ,求
,求 (
( 为坐标原点)的面积最小时
为坐标原点)的面积最小时 的值,并求出面积的最小值.
的值,并求出面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x﹣
 .
.
(1)讨论f(x)的单调性.
(2)若f(x)在区间(1,2)上单调递减,求实数a的取值范围. -
科目: 来源: 题型:
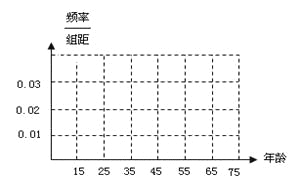
查看答案和解析>>【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
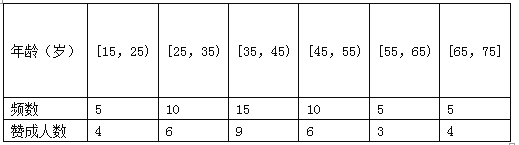
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为
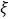 ,求随机变量
,求随机变量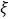 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,已知四边形
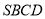 是由直角△
是由直角△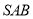 和直角梯形
和直角梯形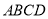 拼接而成的,其中
拼接而成的,其中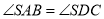
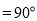 .且点
.且点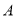 为线段
为线段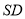 的中点,
的中点, 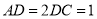 ,
, 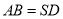 现将△
现将△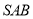 沿
沿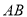 进行翻折,使得二面角
进行翻折,使得二面角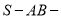
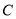 的大小为
的大小为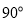 ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接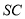 ,点
,点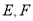 分别在线段
分别在线段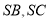 上.
上.

(1)证明:
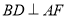 ;
;(2)若三棱锥
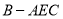 的体积为四棱锥
的体积为四棱锥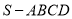 体积的
体积的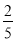 ,求点
,求点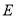 到平面
到平面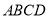 的距离.
的距离.
相关试题

