【题目】在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称,若sinα= ![]() ,则cos(α﹣β)= .
,则cos(α﹣β)= .
参考答案:
【答案】﹣ ![]()
【解析】解:方法一:∵角α与角β均以Ox为始边,它们的终边关于y轴对称,
∴sinα=sinβ= ![]() ,cosα=﹣cosβ,
,cosα=﹣cosβ,
∴cos(α﹣β)=cosαcosβ+sinαsinβ=﹣cos2α+sin2α=2sin2α﹣1= ![]() ﹣1=﹣
﹣1=﹣ ![]()
方法二:∵sinα= ![]() ,
,
当α在第一象限时,cosα= ![]() ,
,
∵α,β角的终边关于y轴对称,
∴β在第二象限时,sinβ=sinα= ![]() ,cosβ=﹣cosα=﹣
,cosβ=﹣cosα=﹣ ![]() ,
,
∴cos(α﹣β)=cosαcosβ+sinαsinβ=﹣ ![]() ×
× ![]() +
+ ![]() ×
× ![]() =﹣
=﹣ ![]()
:∵sinα= ![]() ,
,
当α在第二象限时,cosα=﹣ ![]() ,
,
∵α,β角的终边关于y轴对称,
∴β在第一象限时,sinβ=sinα= ![]() ,cosβ=﹣cosα=
,cosβ=﹣cosα= ![]() ,
,
∴cos(α﹣β)=cosαcosβ+sinαsinβ=﹣ ![]() ×
× ![]() +
+ ![]() ×
× ![]() =﹣
=﹣ ![]()
综上所述cos(α﹣β)=﹣ ![]() ,
,
所以答案是:﹣ ![]()
【考点精析】掌握同角三角函数基本关系的运用和两角和与差的余弦公式是解答本题的根本,需要知道同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() ;两角和与差的余弦公式:
;两角和与差的余弦公式:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x∈[-
 ,
,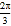 ],
],(1)求函数y=cosx的值域;
(2)求函数y=-3sin2x-4cosx+4的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
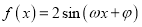 (其中
(其中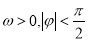 ),若函数
),若函数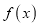 的图象与
的图象与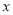 轴的任意两个相邻交点间的距离为
轴的任意两个相邻交点间的距离为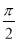 ,且函数
,且函数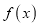 的图象过点
的图象过点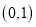 .
.(1)求
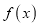 的解析式;
的解析式;(2)求
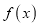 的单调增区间:
的单调增区间:(3)求
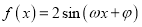 在
在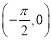 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】设实数
 ,
,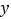 满足约束条件
满足约束条件 ,则
,则 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C. 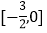 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,
 =9a2a6.
=9a2a6.(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列
 的前n项和.
的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一个平面内,向量
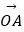 ,
, 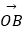 ,
, 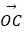 的模分别为1,1,
的模分别为1,1,  ,
, 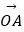 与
与 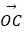 的夹角为α,且tanα=7,
的夹角为α,且tanα=7, 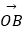 与
与 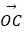 的夹角为45°.若
的夹角为45°.若 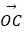 =m
=m 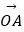 +n
+n 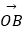 (m,n∈R),则m+n= .
(m,n∈R),则m+n= . 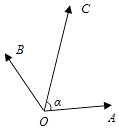
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=sin(ωx﹣
 )+sin(ωx﹣
)+sin(ωx﹣  ),其中0<ω<3,已知f(
),其中0<ω<3,已知f(  )=0.(12分)
)=0.(12分)
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 个单位,得到函数y=g(x)的图象,求g(x)在[﹣
个单位,得到函数y=g(x)的图象,求g(x)在[﹣  ,
, 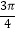 ]上的最小值.
]上的最小值.
相关试题

