【题目】现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是 ![]() ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是 ![]() ,且各题答对与否相互独立.用X表示张同学答对题的个数,求X的分布列和数学期望.
,且各题答对与否相互独立.用X表示张同学答对题的个数,求X的分布列和数学期望.
参考答案:
【答案】
(1)解:设事件A=“张同学至少取到1道乙类题”
则 ![]() =张同学至少取到的全为甲类题
=张同学至少取到的全为甲类题
∴P(A)=1﹣P( ![]() )=1﹣
)=1﹣ ![]() =
= ![]()
(2)解:X的所有可能取值为0,1,2,3
P (X=0)= ![]() =
= ![]()
P(X=1)= ![]() =
= ![]()
P(X=2)= ![]() +
+ ![]() =
= ![]()
P(X=3)= ![]() =
= ![]()
X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
EX= ![]()
【解析】(1)从10道试题中取出3个的所有可能结果数有 ![]() ,张同学至少取到1道乙类题的对立事件是:张同学取到的全为甲类题,代入古典概率的求解公式即可求解(2)先判断随机变量X的所有可能取值为0,1,2,3,根据题意求出随机变量的各个取值的概率,即可求解分布列及期望值
,张同学至少取到1道乙类题的对立事件是:张同学取到的全为甲类题,代入古典概率的求解公式即可求解(2)先判断随机变量X的所有可能取值为0,1,2,3,根据题意求出随机变量的各个取值的概率,即可求解分布列及期望值
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的个数有( )
①用
 刻画回归效果,当
刻画回归效果,当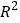 越大时,模型的拟合效果越差;反之,则越好;
越大时,模型的拟合效果越差;反之,则越好;②命题“
 ,
, ”的否定是“
”的否定是“ ,
, ”;
”;③若回归直线的斜率估计值是
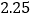 ,样本点的中心为
,样本点的中心为 ,则回归直线方程是
,则回归直线方程是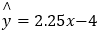 ;
;④综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”。
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,函数
,函数 有四个不同的零点,从小到大依次为
有四个不同的零点,从小到大依次为 ,
, ,
, ,
,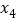 ,则
,则 的取值范围为( )
的取值范围为( )A.
 B.
B.  C.
C.  D.
D. 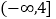
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.

(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求证:二面角C﹣PB﹣A的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线C1:x2=4y,C2:x2=﹣2py(p>0),点M(x0 , y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1﹣
 时,切线MA的斜率为﹣
时,切线MA的斜率为﹣  .
. 
(1)求P的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(1+x)e﹣2x , g(x)=ax+
 +1+2xcosx,当x∈[0,1]时,
+1+2xcosx,当x∈[0,1]时,
(1)求证: ;
;
(2)若f(x)≥g(x)恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为抛物线
为抛物线 的焦点,
的焦点, 为其标准线与
为其标准线与 轴的交点,过
轴的交点,过 的直线交抛物线
的直线交抛物线 于
于 ,
, 两点,
两点, 为线段
为线段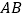 的中点,且
的中点,且 ,则
,则 __________.
__________.
相关试题

