【题目】已知函数f(x)=(1+x)e﹣2x , g(x)=ax+ ![]() +1+2xcosx,当x∈[0,1]时,
+1+2xcosx,当x∈[0,1]时,
(1)求证: ![]() ;
;
(2)若f(x)≥g(x)恒成立,求实数a的取值范围.
参考答案:
【答案】
(1)证明:①当x∈[0,1)时,(1+x)e﹣2x≥1﹣x(1+x)e﹣x≥(1﹣x)ex,
令h(x)=(1+x)e﹣x﹣(1﹣x)ex,则h′(x)=x(ex﹣e﹣x).
当x∈[0,1)时,h′(x)≥0,
∴h(x)在[0,1)上是增函数,
∴h(x)≥h(0)=0,即f(x)≥1﹣x.
②当x∈[0,1)时, ![]() ex≥1+x,令u(x)=ex﹣1﹣x,则u′(x)=ex﹣1.
ex≥1+x,令u(x)=ex﹣1﹣x,则u′(x)=ex﹣1.
当x∈[0,1)时,u′(x)≥0,
∴u(x)在[0,1)单调递增,∴u(x)≥u(0)=0,
∴f(x) ![]() .
.
综上可知: ![]() .
.
(2)解:设G(x)=f(x)﹣g(x)= ![]()
≥ ![]() =
= ![]() .
.
令H(x)= ![]() ,则H′(x)=x﹣2sinx,
,则H′(x)=x﹣2sinx,
令K(x)=x﹣2sinx,则K′(x)=1﹣2cosx.
当x∈[0,1)时,K′(x)<0,
可得H′(x)是[0,1)上的减函数,∴H′(x)≤H′(0)=0,故H(x)在[0,1)单调递减,
∴H(x)≤H(0)=2.∴a+1+H(x)≤a+3.
∴当a≤﹣3时,f(x)≥g(x)在[0,1)上恒成立.
下面证明当a>﹣3时,f(x)≥g(x)在[0,1)上不恒成立.
f(x)﹣g(x)≤ ![]() =
= ![]() =﹣x
=﹣x ![]() .
.
令v(x)= ![]() =
= ![]() ,则v′(x)=
,则v′(x)= ![]() .
.
当x∈[0,1)时,v′(x)≤0,故v(x)在[0,1)上是减函数,
∴v(x)∈(a+1+2cos1,a+3].
当a>﹣3时,a+3>0.
∴存在x0∈(0,1),使得v(x0)>0,此时,f(x0)<g(x0).
即f(x)≥g(x)在[0,1)不恒成立.
综上实数a的取值范围是(﹣∞,﹣3].
【解析】(1)①当x∈[0,1)时,(1+x)e﹣2x≥1﹣x(1+x)e﹣x≥(1﹣x)ex , 令h(x)=(1+x)e﹣x﹣(1﹣x)ex , 利用导数得到h(x)的单调性即可证明;②当x∈[0,1)时, ![]() ex≥1+x,令u(x)=ex﹣1﹣x,利用导数得出h(x)的单调性即可证明.(2)利用(I)的结论得到f(x)≥1﹣x,于是G(x)=f(x)﹣g(x)≥
ex≥1+x,令u(x)=ex﹣1﹣x,利用导数得出h(x)的单调性即可证明.(2)利用(I)的结论得到f(x)≥1﹣x,于是G(x)=f(x)﹣g(x)≥ ![]() =
= ![]() .再令H(x)=
.再令H(x)= ![]() ,通过多次求导得出其单调性即可求出a的取值范围.
,通过多次求导得出其单调性即可求出a的取值范围.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.

(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求证:二面角C﹣PB﹣A的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是  ,且各题答对与否相互独立.用X表示张同学答对题的个数,求X的分布列和数学期望.
,且各题答对与否相互独立.用X表示张同学答对题的个数,求X的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线C1:x2=4y,C2:x2=﹣2py(p>0),点M(x0 , y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1﹣
 时,切线MA的斜率为﹣
时,切线MA的斜率为﹣  .
. 
(1)求P的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为抛物线
为抛物线 的焦点,
的焦点, 为其标准线与
为其标准线与 轴的交点,过
轴的交点,过 的直线交抛物线
的直线交抛物线 于
于 ,
, 两点,
两点, 为线段
为线段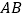 的中点,且
的中点,且 ,则
,则 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是某港口水的深度
是某港口水的深度 (单位:
(单位: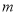 )关于时间
)关于时间 的函数,其中
的函数,其中 .下表是该港口某一天从
.下表是该港口某一天从 时至
时至 时记录的时间
时记录的时间 与水深
与水深 的关系:
的关系:t
0
3
6
9
12
15
18
21
24
y
5.0
7.5
5.0
2.5
5.0
7.5
5.0
2.5
5.0
经长期观察,函数
 的图像可以近似看成函数
的图像可以近似看成函数 的图像.最能近似表示表中数据间对应关系的函数是__________.
的图像.最能近似表示表中数据间对应关系的函数是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四面体
 中,
中, ,
,  .
.
(1)证明:
 ;
;(2)若
 ,
, ,四面体
,四面体 的体积为2,求二面角
的体积为2,求二面角 的余弦值.
的余弦值.
相关试题

