【题目】已知圆![]() 经过
经过![]() 两点,且圆心
两点,且圆心![]() 在直线
在直线![]() 上.
上.

(1)求圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交截得的弦长为
相交截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)已知点![]() ,在平面内是否存在异于点
,在平面内是否存在异于点![]() 的定点
的定点![]() ,对于圆
,对于圆![]() 上的任意动点
上的任意动点![]() ,都有
,都有![]() 为定值?若存在求出定点
为定值?若存在求出定点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)见解析
;(3)见解析
【解析】
(1)设出圆的一般方程,代入三个条件解得答案.
(2)将弦长转化为圆心到直线的距离,利用点到直线的距离公式得到答案.
(3)设出点![]() 利用两点间距离公式得到比值关系,设为
利用两点间距离公式得到比值关系,设为![]() ,最后利用方程与N无关得到关系式计算得到答案.
,最后利用方程与N无关得到关系式计算得到答案.
(1)因为圆![]() 经过
经过![]() 两点,且圆心
两点,且圆心![]() 在直线
在直线![]() 上
上
设圆![]() :
:![]()
所以![]() ,
,![]() ,
,![]()
所以![]() ,
,![]()
所以圆![]()
(2)当斜率不存在的时候,![]() ,弦长为
,弦长为![]() ,满足题意
,满足题意
当斜率存在的时候,设![]() ,即
,即![]()
![]()
所以直线![]() 的方程为:
的方程为:![]() 或
或![]()
(3)设![]() ,且
,且![]()
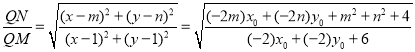
因为![]() 为定值,设
为定值,设![]()
化简得:![]() ,与
,与![]() 点位置无关,
点位置无关,
所以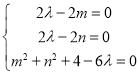
解得:![]() 或
或![]()
所以定点为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在道路边安装路灯,路面
 宽
宽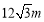 ,灯柱
,灯柱 高14
高14 ,灯杆
,灯杆 与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线
与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线 与灯杆
与灯杆 垂直,轴线
垂直,轴线 ,灯杆
,灯杆 都在灯柱
都在灯柱 和路面宽线
和路面宽线 确定的平面内.
确定的平面内.
(1)当灯杆
 长度为多少时,灯罩轴线
长度为多少时,灯罩轴线 正好通过路面
正好通过路面 的中线?
的中线?(2)如果灯罩轴线AC正好通过路面
 的中线,此时有一高2.5
的中线,此时有一高2.5  的警示牌直立在
的警示牌直立在 处,求警示牌在该路灯灯光下的影子长度.
处,求警示牌在该路灯灯光下的影子长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABD沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.

(Ⅰ)求证:CD⊥A′B;
(Ⅱ)试在线段A′C上确定一点P,使得二面角P﹣BD﹣C的大小为45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办“中国诗词大赛”活动,某班派出甲乙两名选手同时参加比赛.大赛设有15个诗词填空题,其中“唐诗”、“宋词”和“毛泽东诗词”各5个.每位选手从三类诗词中各任选1个进行作答,3个全答对选手得3分,答对2个选手得2分,答对1个选手得1分,一个都没答对选手得0分.已知“唐诗”、“宋词”和“毛泽东诗词”中甲能答对的题目个数依次为5,4,3,乙能答对的题目个数依此为4,5,4,假设每人各题答对与否互不影响,甲乙两人答对与否也互不影响. 求:
(Ⅰ)甲乙两人同时得到3分的概率;
(Ⅱ)甲乙两人得分之和ξ的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,对任意的
,对任意的 ,满足
,满足 ,其中
,其中 ,
, 为常数.
为常数.(1)若
 的图象在
的图象在 处的切线经过点
处的切线经过点 ,求
,求 的值;
的值;(2)已知
 ,求证
,求证 ;
;(3)当
 存在三个不同的零点时,求
存在三个不同的零点时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,近日我渔船编队在岛
 周围海域作业,在岛
周围海域作业,在岛 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站 ,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与
,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与 相距31海里的
相距31海里的 处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛
处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛 直线航行以保护我渔船编队,30分钟后到达
直线航行以保护我渔船编队,30分钟后到达 处,此时观测站测得
处,此时观测站测得 间的距离为21海里.
间的距离为21海里.
(Ⅰ)求
 的值;
的值;(Ⅱ)试问海警船再向前航行多少分钟方可到岛
 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 的一段图像如图所示.
的一段图像如图所示.
(1)求此函数的解析式;
(2)求此函数在
 上的单调递增区间.
上的单调递增区间.
相关试题

