【题目】已知三个点A(2,1)、B(3,2)、D(﹣1,4).
(1)求证: ![]() ;
;
(2)要使四边形ABCD为矩形,求点C的坐标,并求矩形ABCD两对角线所夹锐角的余弦值.
参考答案:
【答案】
(1)证明:A(2,1),B(3,2),D(﹣1,4).
∴ ![]() =(1,1),
=(1,1), ![]() =(﹣3,3).
=(﹣3,3).
又∵ ![]() =1×(﹣3)+1×3=0,
=1×(﹣3)+1×3=0,
∴ ![]() .
.
(2)解:∵ ![]() ,若四边形ABCD为矩形,则
,若四边形ABCD为矩形,则 ![]() .
.
设C点的坐标为(x,y),则有(1,1)=(x+1,y﹣4),
∴ ![]()
即 ![]()
∴点C的坐标为(0,5).
由于 ![]() =(﹣2,4),
=(﹣2,4), ![]() =(﹣4,2),
=(﹣4,2),
∴ ![]() =(﹣2)×(﹣4)+4×2=16,
=(﹣2)×(﹣4)+4×2=16, ![]() =2
=2 ![]() .
.
设对角线AC与BD的夹角为θ,则cosθ= ![]() =
= ![]() >0.
>0.
故矩形ABCD两条对角线所夹锐角的余弦值为 ![]() .
.
【解析】(1)运用平面向量的数量积得出 ![]() =1×(﹣3)+1×3=0,求解即可.(2)
=1×(﹣3)+1×3=0,求解即可.(2) ![]() .
. ![]() ,坐标得出点C的坐标为(0,5).再运用数量积求解得出cosθ=
,坐标得出点C的坐标为(0,5).再运用数量积求解得出cosθ= ![]() =
= ![]() >0.
>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
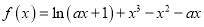 .
.(1)若
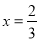 为
为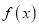 的极值点,求实数
的极值点,求实数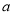 的值;
的值;(2)若
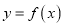 在
在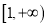 上为增函数,求实数
上为增函数,求实数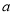 的取值范围;
的取值范围;(2)若
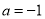 使方程
使方程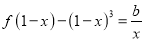 有实根,求实数
有实根,求实数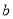 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的奇函数
上的奇函数 满足
满足 ,则不等式
,则不等式 的解集为( )
的解集为( )A.
 B.
B.  C.
C. 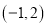 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
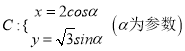 和定点
和定点 ,
, 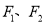 是此曲线的左、右焦点,以原点
是此曲线的左、右焦点,以原点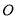 为极点,以
为极点,以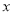 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(1)求直线
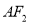 的极坐标方程;
的极坐标方程;(2)经过点
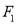 且与直线
且与直线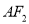 垂直的直线交此圆锥曲线于
垂直的直线交此圆锥曲线于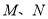 两点,求
两点,求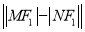 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的程序语句输出的结果S为( )

A.19
B.17
C.15
D.13 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C=
 .
.
(1)若△ABC的面积等于 ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】交警随机抽取了途径某服务站的40辆小型轿车在经过某区间路段的车速(单位:
 ),现将其分成六组为
),现将其分成六组为 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.(1)某小型轿车途经该路段,其速度在
 以上的概率是多少?
以上的概率是多少?(2)若对车速在
 两组内进一步抽测两辆小型轿车,求至少有一辆小型轿车速度在
两组内进一步抽测两辆小型轿车,求至少有一辆小型轿车速度在 内的概率.
内的概率.
相关试题

