【题目】已知函数![]() .
.
(1)若![]() 为
为![]() 的极值点,求实数
的极值点,求实数![]() 的值;
的值;
(2)若![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 使方程
使方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)求导![]() 若
若![]() 为
为![]() 的极值点,则
的极值点,则![]() 从而求得结果.(2)由f(x)在[1,+∞)上为增函数,则有f′(x)≥0,x∈[1,+∞)上恒成立求解.若
从而求得结果.(2)由f(x)在[1,+∞)上为增函数,则有f′(x)≥0,x∈[1,+∞)上恒成立求解.若![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上为增函数成立,若
上为增函数成立,若![]() ,
,
![]() 对
对![]() 上恒成立. 对称轴为
上恒成立. 对称轴为![]() ,从而
,从而![]() 在
在![]() 上为增函数. 只要
上为增函数. 只要![]() 即可(3)将a=-1代入,方程f(1x)(1x)3=
即可(3)将a=-1代入,方程f(1x)(1x)3=![]() 可转化为b=xlnx+x2-x3,x>0上有解,只要求得函数g(x)=xlnx+x2-x3的值域即可.
可转化为b=xlnx+x2-x3,x>0上有解,只要求得函数g(x)=xlnx+x2-x3的值域即可.
试题解析:
(1)![]()
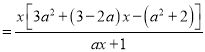
∵![]() 为
为![]() 的极值点,∴
的极值点,∴![]()
∴![]() 且
且![]() ∴
∴![]()
又当![]() 时,
时, ![]() ,从而
,从而![]() 为
为![]() 的极值点成立.
的极值点成立.
(2)因为![]() 在
在![]() 上为增函数,
上为增函数,
所以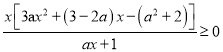 在
在![]() 上恒成立.
上恒成立.
若![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上为增函数成立
上为增函数成立
若![]() ,由
,由![]() 对
对![]() 恒成立知
恒成立知![]() .
.
所以![]() 对
对![]() 上恒成立.
上恒成立.
令![]() ,其对称轴为
,其对称轴为![]() ,
,
因为![]() ,所以
,所以![]() ,从而
,从而![]() 在
在![]() 上为增函数.
上为增函数.
所以只要![]() 即可,即
即可,即![]()
所以![]() 又因为
又因为![]()
(3)若![]() 时,方程
时,方程![]()
可得![]()
即![]() 在
在![]() 上有解
上有解
即求函数![]() 的值域.
的值域.
![]() 令
令![]()
由![]() ∵
∵![]() ∴当
∴当![]() 时,
时, ![]() ,
,
从而![]() 在
在![]() 上为增函数;当
上为增函数;当![]() 时,
时, ![]() ,从而
,从而![]() 在
在![]() 上为减函数.
上为减函数.
∴![]() ,而
,而![]() 可以无穷小.∴
可以无穷小.∴![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asinB=
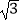 b.
b.
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=
 ,SA=SC=SD=2.
,SA=SC=SD=2.
(I)求证:AC⊥SD;
(Ⅱ)求二面角A﹣SB﹣C的余弦值.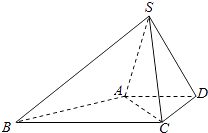
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C1的圆心在坐标原点O,且恰好与直线l1:x﹣2y+3
 =0相切,点A为圆上一动点,AM⊥x轴于点M,且动点N满足
=0相切,点A为圆上一动点,AM⊥x轴于点M,且动点N满足  ,设动点N的轨迹为曲线C.
,设动点N的轨迹为曲线C.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于不同两点A,B,且满足 (O为坐标原点),求线段AB长度的取值范围.
(O为坐标原点),求线段AB长度的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的奇函数
上的奇函数 满足
满足 ,则不等式
,则不等式 的解集为( )
的解集为( )A.
 B.
B.  C.
C. 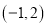 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
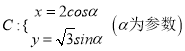 和定点
和定点 ,
, 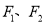 是此曲线的左、右焦点,以原点
是此曲线的左、右焦点,以原点 为极点,以
为极点,以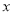 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(1)求直线
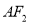 的极坐标方程;
的极坐标方程;(2)经过点
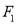 且与直线
且与直线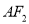 垂直的直线交此圆锥曲线于
垂直的直线交此圆锥曲线于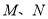 两点,求
两点,求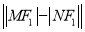 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三个点A(2,1)、B(3,2)、D(﹣1,4).
(1)求证: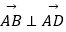 ;
;
(2)要使四边形ABCD为矩形,求点C的坐标,并求矩形ABCD两对角线所夹锐角的余弦值.
相关试题

