【题目】设二次函数f(x)=ax2+bx.
(1)若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围;
(2)当b=1时,若对任意x∈[0,1],-1≤f(x)≤1恒成立,求实数a的取值范围.
参考答案:
【答案】(1)5≤f(-2)≤10;(2)[-2,0).
【解析】
(1)用![]() 和
和![]() 表示
表示![]() ,再根据不等式的性质求得.
,再根据不等式的性质求得.
(2)对![]() 进行参变分离,根据
进行参变分离,根据 ![]() 和
和![]() 求得.
求得.
解 (1)方法一 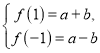
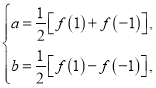
∵f(-2)=4a-2b=3f(-1)+f(1),且1≤f(-1)≤2,2≤f(1)≤4,∴5≤f(-2)≤10.
方法二 设f(-2)=mf(-1)+nf(1),
即4a-2b=m(a-b)+n(a+b)=(m+n)a-(m-n)b,比较两边系数:![]()
![]()
∴f(-2)=3f(-1)+f(1),
下同方法一.
(2)当x∈[0,1]时,-1≤f(x)≤1,即-1≤ax2+x≤1,
即当x∈[0,1]时,ax2+x+1≥0且ax2+x-1≤0恒成立;
当x=0时,显然,ax2+x+1≥0且ax2+x-1≤0均成立;
当x∈(0,1]时,若ax2+x+1≥0恒成立,则a≥-![]() -
-![]() =-(
=-(![]() +
+![]() )2+
)2+![]() ,
,
而-(![]() +
+![]() )2+
)2+![]() 在x∈(0,1]上的最大值为-2,∴a≥-2;
在x∈(0,1]上的最大值为-2,∴a≥-2;
当x∈(0,1]时,ax2+x-1≤0恒成立,则a≤![]() -
-![]() =(
=(![]() -
-![]() )2-
)2-![]() ,
,
而(![]() -
-![]() )2-
)2-![]() 在x∈(0,1]上的最小值为0,∴a≤0,
在x∈(0,1]上的最小值为0,∴a≤0,
∴-2≤a≤0,而a≠0,因此所求a的取值范围为[-2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1 , C2的四个交点按纵坐标从大到小依次为A,B,C,D,记
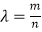 ,△BDM和△ABN的面积分别为S1和S2 .
,△BDM和△ABN的面积分别为S1和S2 . 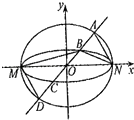
(1)当直线l与y轴重合时,若S1=λS2 , 求λ的值;
(2)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}满足a1=2,an+1-an=3·22n-1.
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n项和Sn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是
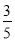 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是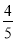 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用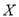 表示张同学答对题的个数,求
表示张同学答对题的个数,求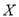 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设n是正整数,r为正有理数.
(1)求函数f(x)=(1+x)r+1﹣(r+1)x﹣1(x>﹣1)的最小值;
(参考数据: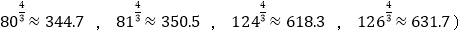 .
.
(2)证明: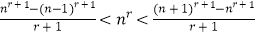 ;
;
(3)设x∈R,记[x]为不小于x的最小整数,例如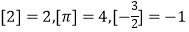 .令
.令 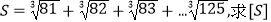 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,求
时,求 的极值;
的极值;(2)当
 时,讨论
时,讨论 的单调性;
的单调性;(3)若对任意的
 ,
, ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某个产品有若干零部件构成,加工时需要经过7道工序,分别记为
 .其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系,若加工工序
.其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系,若加工工序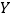 必须要在工序
必须要在工序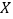 完成后才能开工,则称
完成后才能开工,则称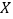 为
为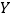 的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:工序







加工时间
3
4
2
2
2
1
5
紧前工序
无

无




现有两台性能相同的生产机器同时加工该产品,则完成该产品的最短加工时间是( )
(假定每道工序只能安排在一台机器上,且不能间断.)
A. 11个小时 B. 10个小时 C. 9个小时 D. 8个小时
相关试题

