【题目】如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1 , C2的四个交点按纵坐标从大到小依次为A,B,C,D,记 ![]() ,△BDM和△ABN的面积分别为S1和S2 .
,△BDM和△ABN的面积分别为S1和S2 . 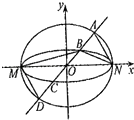
(1)当直线l与y轴重合时,若S1=λS2 , 求λ的值;
(2)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2?并说明理由.
参考答案:
【答案】
(1)解:以题意可设椭圆C1和C2的方程分别为
![]() ,
, ![]() .其中a>m>n>0,
.其中a>m>n>0,
![]() >1.
>1.
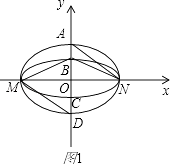
如图1,若直线l与y轴重合,即直线l的方程为x=0,则
![]() ,
,
![]() ,
,
所以 ![]() .
.
在C1和C2的方程中分别令x=0,可得yA=m,yB=n,yD=﹣m,
于是 ![]() .
.
若 ![]() ,则
,则 ![]() ,化简得λ2﹣2λ﹣1=0,由λ>1,解得
,化简得λ2﹣2λ﹣1=0,由λ>1,解得 ![]() .
.
故当直线l与y轴重合时,若S1=λS2,则 ![]() .
.
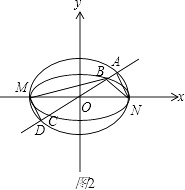
(2)解:如图2,若存在与坐标轴不重合的直线l,使得S1=λS2,根据对称性,
不妨设直线l:y=kx(k>0),
点M(﹣a,0),N(a,0)到直线l的距离分别为d1,d2,则
![]() ,所以d1=d2.
,所以d1=d2.
又 ![]() ,所以
,所以 ![]() ,即|BD|=λ|AB|.
,即|BD|=λ|AB|.
由对称性可知|AB|=|CD|,所以|BC|=|BD|﹣|AB|=(λ﹣1)|AB|,
|AD|=|BD|+|AB|=(λ+1)|AB|,于是 ![]() .
.
将l的方程分别与C1和C2的方程联立,可求得
![]()
根据对称性可知xC=﹣xB,xD=﹣xA,于是
![]() ②
②
从而由①和②可得
![]() ③
③
令 ![]() ,则由m>n,可得t≠1,于是由③可得
,则由m>n,可得t≠1,于是由③可得 ![]() .
.
因为k≠0,所以k2>0.于是③关于k有解,当且仅当 ![]() ,
,
等价于 ![]() ,由λ>1,解得
,由λ>1,解得 ![]() ,
,
即 ![]() ,由λ>1,解得
,由λ>1,解得 ![]() ,所以
,所以
当 ![]() 时,不存在与坐标轴不重合的直线l,使得S1=λS2;
时,不存在与坐标轴不重合的直线l,使得S1=λS2;
当 ![]() 时,存在与坐标轴不重合的直线l,使得S1=λS2.
时,存在与坐标轴不重合的直线l,使得S1=λS2.
【解析】(1)设出两个椭圆的方程,当直线l与y轴重合时,求出△BDM和△ABN的面积S1和S2 , 直接由面积比=λ列式求λ的值;(2)假设存在与坐标轴不重合的直线l,使得S1=λS2 , 设出直线方程,由点到直线的距离公式求出M和N到直线l的距离,利用数学转化思想把两个三角形的面积比转化为线段长度比,由弦长公式得到线段长度比的另一表达式,两式相等得到 ![]() ,换元后利用非零的k值存在讨论λ的取值范围.
,换元后利用非零的k值存在讨论λ的取值范围.
【考点精析】关于本题考查的点到直线的距离公式,需要了解点![]() 到直线
到直线![]() 的距离为:
的距离为: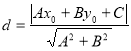 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
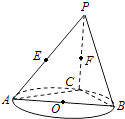
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足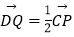 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ. -
科目: 来源: 题型:
查看答案和解析>>【题目】假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量.记一天中从甲地去乙地的旅客人数不超过900的概率为p0 .
(1)求p0的值;
(参考数据:若X~N(μ,σ2),有P(μ﹣σ<X≤μ+σ)=0.6826,P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣3σ<X≤μ+3σ)=0.9974.)
(2)某客运公司用A,B两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次,A,B两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1600元/辆和2400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B型车不多于A型车7辆.若每天要以不小于p0的概率运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A型车、B型车各多少辆? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
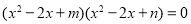 的四个根组成一个首项为
的四个根组成一个首项为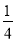 的等差数列,则
的等差数列,则 _____.
_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}满足a1=2,an+1-an=3·22n-1.
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n项和Sn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是
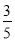 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是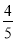 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用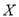 表示张同学答对题的个数,求
表示张同学答对题的个数,求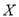 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数f(x)=ax2+bx.
(1)若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围;
(2)当b=1时,若对任意x∈[0,1],-1≤f(x)≤1恒成立,求实数a的取值范围.
相关试题

