【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成![]() 小块地,在总共
小块地,在总共![]() 小块地中,随机选
小块地中,随机选![]() 小块地种植品种甲,另外
小块地种植品种甲,另外![]() 小块地种植品种乙.
小块地种植品种乙.
(1)假设![]() ,求第一大块地都种植品种甲的概率;
,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成![]() 小块,即
小块,即![]() ,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
甲 |
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
参考答案:
【答案】(1)![]() ;(2)应该选择种植品种乙.
;(2)应该选择种植品种乙.
【解析】
试题分析:(1)设事件A为“第一大块地都种品种甲”,求出从![]() 小块地中任选
小块地中任选![]() 小块地种植品种甲的基本事件个数和事件
小块地种植品种甲的基本事件个数和事件![]() 包含的基本事件的个数,由古典概型的概率计算公式求出
包含的基本事件的个数,由古典概型的概率计算公式求出![]() ;(2)分别求出甲、乙两个品种每公顷产量的样本平均数和样本方差,通过对比选择种植平均数较大且方差较小的品种,但本题中甲、乙两个品种的方差接近,所以要选平均数较大的乙品种.对于求概率问题,首先要判断题目涉及的事件的概率类型,选用恰当的概率公式进行计算,其次在求出概率后,要对题中问题进行回答.在用统计方法比较两类对象优劣时,既要考虑平均水平(均值),又要考虑稳定性(方差)。
;(2)分别求出甲、乙两个品种每公顷产量的样本平均数和样本方差,通过对比选择种植平均数较大且方差较小的品种,但本题中甲、乙两个品种的方差接近,所以要选平均数较大的乙品种.对于求概率问题,首先要判断题目涉及的事件的概率类型,选用恰当的概率公式进行计算,其次在求出概率后,要对题中问题进行回答.在用统计方法比较两类对象优劣时,既要考虑平均水平(均值),又要考虑稳定性(方差)。
试题解析:(1)设第一大块地中的两小块地编号为![]() ,
,![]() ,第二大块地中的两小块地编号为
,第二大块地中的两小块地编号为![]() ,
,![]() ,令事件A为“第一大块地都种品种甲”. 2分
,令事件A为“第一大块地都种品种甲”. 2分
从![]() 小块地中任选
小块地中任选![]() 小块地种植品种甲的基本事件共
小块地种植品种甲的基本事件共![]() 个:
个:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
而事件A包含1个基本事件:![]() . 4分
. 4分
由古典概型概率计算公式可知,![]() . 6分
. 6分
(2)品种甲的每公顷产量的样本平均数和样本方差分别为:
![]() , 7分
, 7分
![]() . 8分
. 8分
品种乙的每公顷产量的样本平均数和样本方差分别为:
![]() , 9分
, 9分
![]() 10分
10分
由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差差异不大,故应该选择种植品种乙. 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)(万元)满足R(x)=
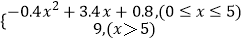 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)要使甲厂有盈利,求产量x的范围;
(3)甲厂生产多少台产品时,可使盈利最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=a﹣
 为奇函数.
为奇函数.
(1)求a的值;
(2)试判断函数f(x)在(﹣∞,+∞)上的单调性,并证明你的结论;
(3)若对任意的t∈R,不等式f[t2﹣(m﹣2)t]+f(t2﹣m+1)>0恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 的圆心在直线
的圆心在直线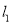 :
: 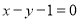 上,与直线
上,与直线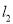 :
:  相切,且截直线
相切,且截直线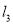 :
: 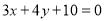 所得弦长为6
所得弦长为6(Ⅰ)求圆
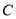 的方程
的方程(Ⅱ)过点
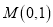 是否存在直线
是否存在直线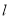 ,使以
,使以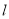 被圆
被圆 截得弦
截得弦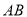 为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由.
为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
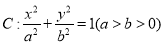 ,定义椭圆
,定义椭圆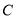 上的点
上的点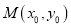 的“伴随点”为
的“伴随点”为 .
.(1)求椭圆
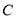 上的点
上的点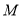 的“伴随点”
的“伴随点”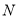 的轨迹方程;
的轨迹方程; (2)如果椭圆
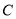 上的点
上的点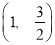 的“伴随点”为
的“伴随点”为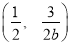 ,对于椭圆
,对于椭圆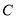 上的任意点
上的任意点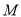 及它的“伴随点”
及它的“伴随点”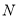 ,求
,求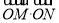 的取值范围;
的取值范围;(3)当
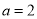 ,
, 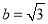 时,直线
时,直线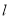 交椭圆
交椭圆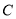 于
于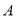 ,
, 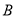 两点,若点
两点,若点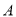 ,
, 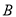 的“伴随点”分别是
的“伴随点”分别是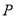 ,
, 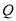 ,且以
,且以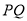 为直径的圆经过坐标原点
为直径的圆经过坐标原点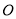 ,求
,求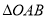 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产
 ,
,  ,
,  三种玩具共100个,且
三种玩具共100个,且 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:玩具名称



工时(分钟)
5
7
4
利润(元)
5
6
3
(Ⅰ)用每天生产
 种玩具个数
种玩具个数 与
与 种玩具
种玩具 表示每天的利润
表示每天的利润 (元);
(元);(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
相关试题

