【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
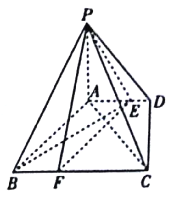
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
【解析】试题分析:(Ⅰ)现根据已知,结合平面几何知识证明![]() ,进而可证四边形
,进而可证四边形![]() 是平行四边形,则
是平行四边形,则![]() ,从而
,从而![]() ,利用
,利用![]() 底面
底面![]() ,结合线面垂直、面面垂直的判定定理可得结果;(Ⅱ)以
,结合线面垂直、面面垂直的判定定理可得结果;(Ⅱ)以![]() 为坐标原点建立如图所示的空间直角坐标系,∵
为坐标原点建立如图所示的空间直角坐标系,∵![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
再求出平面![]() 的一个法向量,利用空间向量夹角余弦公式可得结果.
的一个法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(Ⅰ)∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∵底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∴四边形![]() 是平行四边形,则
是平行四边形,则![]() ,
,
∴![]() ,
,
∵![]() 底面
底面![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)解:∵![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,则
,则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
若![]() 与平面
与平面![]() 所成夹角为
所成夹角为![]() ,则
,则![]() ,即
,即![]() ,
,
取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]() ,以
,以![]() 为坐标原点建立如图所示的空间直角坐标系
为坐标原点建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则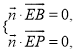 即
即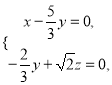
令![]() ,则
,则![]() ,
, ![]() ,∴
,∴![]() ,
,
∵![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴![]() ,
,
即当二面角![]() 的余弦值为
的余弦值为![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
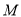 :
: 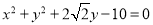 和点
和点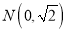 ,动圆
,动圆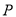 经过点
经过点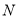 且与圆
且与圆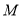 相切,圆心
相切,圆心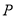 的轨迹为曲线
的轨迹为曲线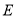 .
.(1)求曲线
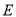 的方程;
的方程;(2)点
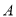 是曲线
是曲线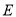 与
与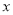 轴正半轴的交点,点
轴正半轴的交点,点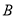 ,
, 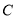 在曲线
在曲线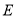 上,若直线
上,若直线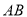 ,
, 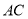 的斜率分别是
的斜率分别是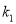 ,
, 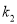 ,满足
,满足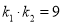 ,求
,求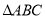 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x , x∈(0,2)的值域为A,函数g(x)=log2(x﹣2a)+
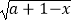 (a<1)的定义域为B.
(a<1)的定义域为B.
(1)求集合A,B;
(2)若BA,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从
 个招标问题中随机抽取
个招标问题中随机抽取 个问题,已知这
个问题,已知这 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.(1)求甲、乙两家公司共答对
 道题目的概率;
道题目的概率;(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某蔬菜商店买进的土豆
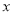 (吨)与出售天数
(吨)与出售天数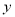 (天)之间的关系如表所示:
(天)之间的关系如表所示: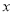
2
3
4
5
6
7
9
12
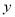
1
2
3
3
4
5
6
8
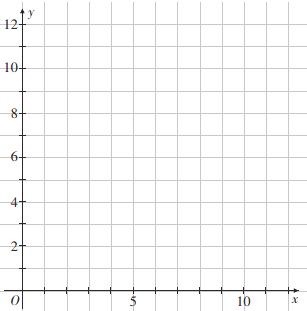
(Ⅰ)请根据表中数据在所给网格中绘制散点图;
(Ⅱ)请根据表中提供的数据,用最小二乘法求出
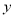 关于
关于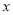 的线性回归方程
的线性回归方程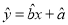 (其中
(其中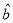 保留2位有效数字);
保留2位有效数字);(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附:
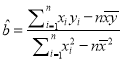 ,
, 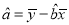 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a是实数,f(x)=a﹣
 (x∈R).
(x∈R).
(1)证明不论a为何实数,f(x)均为增函数;
(2)若f(x)满足f(﹣x)+f(x)=0,解关于x的不等式f(x+1)+f(1﹣2x)>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)若
 ,求函数
,求函数 的极值;
的极值;(Ⅱ)若
 ,
,  ,
,  ,使得
,使得 (
( ),求实数
),求实数 的取值范围.
的取值范围.
相关试题

