【题目】已知函数f(x)=2x , x∈(0,2)的值域为A,函数g(x)=log2(x﹣2a)+ ![]() (a<1)的定义域为B.
(a<1)的定义域为B.
(1)求集合A,B;
(2)若BA,求实数a的取值范围.
参考答案:
【答案】
(1)解:已知函数f(x)=2x,x∈(0,2)的值域为A,
∴A=(1,4),
函数g(x)=log2(x﹣2a)+ ![]() (a<1)的定义域为B.
(a<1)的定义域为B.
∴B=(2a,a+1),a<1,
(2)解:若BA,则(2a,a+1)(1,4),
∴ 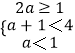 ,解得:
,解得: ![]() ≤a<1
≤a<1
【解析】(1)根据指数函数以及对数函数的性质解出即可;(2)根据集合的包含关系得到关于a的不等式组,解出即可.
【考点精析】通过灵活运用集合的表示方法-特定字母法和函数的定义域及其求法,掌握①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{![]() |
|![]() 具有的性质},其中
具有的性质},其中![]() 为集合的代表元素.④图示法:用数轴或韦恩图来表示集合;求函数的定义域时,一般遵循以下原则:①
为集合的代表元素.④图示法:用数轴或韦恩图来表示集合;求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零即可以解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设关于
 的一元二次方程
的一元二次方程 .
.(1)若
 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,  是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;(2)若
 时从区间
时从区间 上任取的一个数,
上任取的一个数,  是从区间
是从区间 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x),在(0,+∞)内是减函数,又有f(3)=0,则xf(x)<0的解集为( )
A.{x|﹣3<x<0或x>3}
B.{x|x<﹣3或0<x<3}
C.{x|﹣3<x<0或0<x<3}
D.{x|x<﹣3或x>3} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
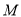 :
: 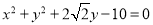 和点
和点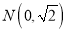 ,动圆
,动圆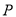 经过点
经过点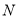 且与圆
且与圆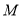 相切,圆心
相切,圆心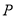 的轨迹为曲线
的轨迹为曲线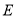 .
.(1)求曲线
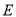 的方程;
的方程;(2)点
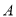 是曲线
是曲线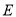 与
与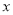 轴正半轴的交点,点
轴正半轴的交点,点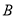 ,
, 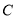 在曲线
在曲线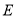 上,若直线
上,若直线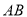 ,
, 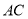 的斜率分别是
的斜率分别是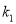 ,
, 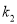 ,满足
,满足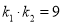 ,求
,求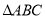 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从
 个招标问题中随机抽取
个招标问题中随机抽取 个问题,已知这
个问题,已知这 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.(1)求甲、乙两家公司共答对
 道题目的概率;
道题目的概率;(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
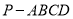 中,
中, 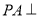 底面
底面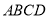 ,底面
,底面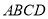 是直角梯形,
是直角梯形,  ,
, 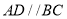 ,
, 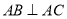 ,
, 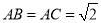 ,点
,点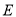 在
在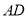 上,且
上,且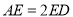 .
.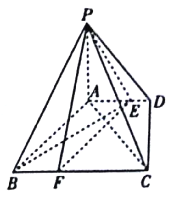
(Ⅰ)已知点
 在
在 上,且
上,且 ,求证:平面
,求证:平面 平面
平面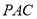 ;
;(Ⅱ)当二面角
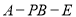 的余弦值为多少时,直线
的余弦值为多少时,直线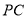 与平面
与平面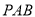 所成的角为
所成的角为 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某蔬菜商店买进的土豆
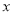 (吨)与出售天数
(吨)与出售天数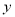 (天)之间的关系如表所示:
(天)之间的关系如表所示: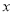
2
3
4
5
6
7
9
12
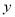
1
2
3
3
4
5
6
8
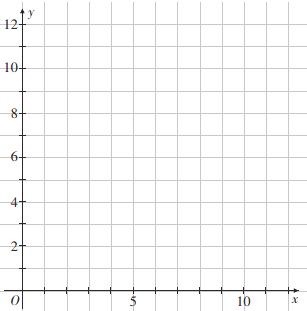
(Ⅰ)请根据表中数据在所给网格中绘制散点图;
(Ⅱ)请根据表中提供的数据,用最小二乘法求出
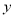 关于
关于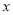 的线性回归方程
的线性回归方程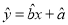 (其中
(其中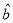 保留2位有效数字);
保留2位有效数字);(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附:
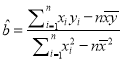 ,
, 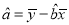 .
.
相关试题

