【题目】设m个正数a1 , a2 , …,am(m≥4,m∈N*)依次围成一个圆圈.其中a1 , a2 , a3 , …ak﹣1 , ak(k<m,k∈N*)是公差为d的等差数列,而a1 , am , am﹣1 , …,ak+1 , ak是公比为2的等比数列.
(1)若a1=d=2,k=8,求数列a1 , a2 , …,am的所有项的和Sm;
(2)若a1=d=2,m<2015,求m的最大值;
(3)是否存在正整数k,满足a1+a2+…+ak﹣1+ak=3(ak+1+ak+2+…+am﹣1+am)?若存在,求出k值;若不存在,请说明理由.
参考答案:
【答案】
(1)解:依题意ak=16,故数列a1,a2,…,am即为2,4,6,8,10,12,14,16,8,4共10个数,
此时m=10,Sm=84
(2)解:由数列{an}满足a1=d=2,是首项为2、公差为2的等差数列知,ak=2k,
而a1,am,am﹣1,…,ak+1,ak是首项为2、公比为2的等比数列知, ![]() ,
,
故有2k=2m+2﹣k,k=2m+1﹣k,即k必是2的整数次幂,
由k2k=2m+1知,要使m最大,k必须最大,
又k<m<2015,故k的最大值210,
从而21021024=2m+1,m的最大值是1033
(3)解:由数列{an}是公差为d的等差数列知,ak=a1+(k﹣1)d,
而a1,am,am﹣1,…,ak+1,ak是公比为2的等比数列 ![]() ,
,
故a1+(k﹣1)d= ![]() ,
, ![]()
又a1+a2+…ak﹣1+ak=3(ak+ak+1+…+am﹣1+am),am=2a1
则 ![]() ,即
,即 ![]() ,
,
则 ![]() ,即k2m+1﹣k+k=6×2m+1﹣k﹣12,
,即k2m+1﹣k+k=6×2m+1﹣k﹣12,
显然k≠6,则 ![]()
所以k<6,将k=1,2,3,4,5一一代入验证知,
当k=4时,上式右端为8,等式成立,此时m=6,
综上可得:当且仅当m=6时,存在k=4满足等式
【解析】(1)依题意ak=16,故数列a1 , a2 , …,am即为2,4,6,8,10,12,14,16,8,4共10个数,即可得出.(2)由数列{an}满足a1=d=2,利用等差数列的通项公式可得ak=2k.而a1 , am , am﹣1 , …,ak+1 , ak是首项为2、公比为2的等比数列知, ![]() .故有2k=2m+2﹣k , k=2m+1﹣k , 即k必是2的整数次幂,由k2k=2m+1知,要使m最大,k必须最大,又k<m<2015,故k的最大值210 , 即可得出.(3)由数列{an}是公差为d的等差数列知,ak=a1+(k﹣1)d,而a1 , am , am﹣1 , …,ak+1 , ak是公比为2的等比数列
.故有2k=2m+2﹣k , k=2m+1﹣k , 即k必是2的整数次幂,由k2k=2m+1知,要使m最大,k必须最大,又k<m<2015,故k的最大值210 , 即可得出.(3)由数列{an}是公差为d的等差数列知,ak=a1+(k﹣1)d,而a1 , am , am﹣1 , …,ak+1 , ak是公比为2的等比数列 ![]() ,a1+(k﹣1)d=
,a1+(k﹣1)d= ![]() ,
, ![]() ,又a1+a2+…ak﹣1+ak=3(ak+ak+1+…+am﹣1+am),am=2a1 , 显然k≠6,则
,又a1+a2+…ak﹣1+ak=3(ak+ak+1+…+am﹣1+am),am=2a1 , 显然k≠6,则 ![]() ,所以k<6,代入验证即可得出.
,所以k<6,代入验证即可得出.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级, 一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
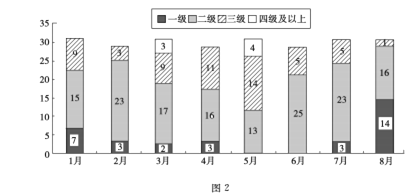
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比,空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】当
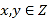 ,则称点
,则称点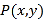 为平面上单调格点:设
为平面上单调格点:设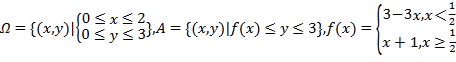
求从区域
 中任取一点
中任取一点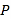 ,而该点落在区域
,而该点落在区域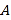 上的概率;
上的概率;求从区域
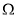 中的所有格点中任取一点
中的所有格点中任取一点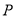 ,而该点是区域
,而该点是区域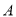 上的格点的概率.
上的格点的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.单位向量都相等
B.若 与
与 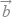 是共线向量,
是共线向量, 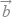 与
与  是共线向量,则
是共线向量,则  与
与  是共线向量
是共线向量
C.| +
+ 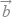 |=|
|=|  ﹣
﹣ 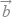 |,则
|,则 
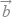 =0
=0
D.若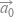 与
与  是单位向量,则
是单位向量,则 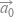
 =1
=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲
 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为 万元,且
万元,且 (
( ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为 (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;(2)为了让年利润
 不低于2360万元,求年产量
不低于2360万元,求年产量 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”

(1)求
 的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率)
的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率) (2)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷
读书迷
合计
男
15
女
45
合计
附:
 .
.
0.100
0.050
0.025
0.010
0.001

2.706
3.841
5.024
6.635
10.828
相关试题

