【题目】下列命题正确的是( )
A.单位向量都相等
B.若 ![]() 与
与 ![]() 是共线向量,
是共线向量, ![]() 与
与 ![]() 是共线向量,则
是共线向量,则 ![]() 与
与 ![]() 是共线向量
是共线向量
C.| ![]() +
+ ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]()
![]() =0
=0
D.若 ![]() 与
与 ![]() 是单位向量,则
是单位向量,则 ![]()
![]() =1
=1
参考答案:
【答案】C
【解析】解:对于A,单位向量是模长为1的向量,它们的方向是任意的,∴单位向量不一定相等,A错误; 对于B,∵零向量与任意向量方向相同,都共线,若 ![]() 是零向量,则
是零向量,则 ![]() 与
与 ![]() 不一定共线,∴B错误;
不一定共线,∴B错误;
对于C,若| ![]() +
+ ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]() +2
+2 ![]()
![]() +
+ ![]() =
= ![]() ﹣2
﹣2 ![]()
![]() +
+ ![]() ,∴4
,∴4 ![]()
![]() =0,即
=0,即 ![]()
![]() =0,∴C正确;
=0,∴C正确;
对于D, ![]() 与
与 ![]() 是单位向量,且夹角为θ,∴
是单位向量,且夹角为θ,∴ ![]()
![]() =1×1×cosθ=cosθ≤1,∴D错误.
=1×1×cosθ=cosθ≤1,∴D错误.
综上,正确的命题是C.
故选:C.
由单位向量与向量相等的定义,判断A是错误的;
由零向量与任意向量方向相同,若 ![]() 是零向量时,B不一定成立;
是零向量时,B不一定成立;
由| ![]() +
+ ![]() |=
|= ![]() ﹣
﹣ ![]() |,推出
|,推出 ![]()
![]() =0,判断C是正确的;
=0,判断C是正确的;
由单位向量与数量积的定义,判断D是错误的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级, 一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
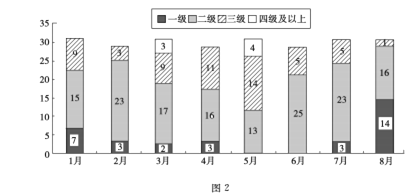
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比,空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】当
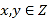 ,则称点
,则称点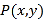 为平面上单调格点:设
为平面上单调格点:设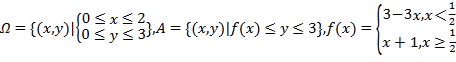
求从区域
 中任取一点
中任取一点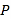 ,而该点落在区域
,而该点落在区域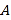 上的概率;
上的概率;求从区域
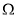 中的所有格点中任取一点
中的所有格点中任取一点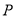 ,而该点是区域
,而该点是区域 上的格点的概率.
上的格点的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设m个正数a1 , a2 , …,am(m≥4,m∈N*)依次围成一个圆圈.其中a1 , a2 , a3 , …ak﹣1 , ak(k<m,k∈N*)是公差为d的等差数列,而a1 , am , am﹣1 , …,ak+1 , ak是公比为2的等比数列.
(1)若a1=d=2,k=8,求数列a1 , a2 , …,am的所有项的和Sm;
(2)若a1=d=2,m<2015,求m的最大值;
(3)是否存在正整数k,满足a1+a2+…+ak﹣1+ak=3(ak+1+ak+2+…+am﹣1+am)?若存在,求出k值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲
 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为 万元,且
万元,且 (
( ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为 (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;(2)为了让年利润
 不低于2360万元,求年产量
不低于2360万元,求年产量 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”

(1)求
 的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率)
的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率) (2)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷
读书迷
合计
男
15
女
45
合计
附:
 .
.
0.100
0.050
0.025
0.010
0.001

2.706
3.841
5.024
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, ,
, ,
, ,平面
,平面 底面
底面 ,
, .
. 和
和 分别是
分别是 和
和 的中点,求证:
的中点,求证:
(Ⅰ)
 底面
底面 ;
;(Ⅱ)
 平面
平面 ;
;(Ⅲ)平面
 平面
平面 .
.
相关试题

