【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() .
.
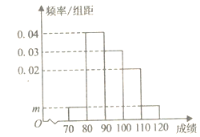
(1)求图中m的值;
(2)根据频率分布直方图,估计这200名学生的平均分(同一组中的数据用该组区间的中间值作代表)和中位数(四舍五入取整数);
(3)若这200名学生的数学成绩中,某些分数段的人数x与英语成绩相应分数段的人数y之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) |
x:y | 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
参考答案:
【答案】(1)![]() (2)平均分为
(2)平均分为![]() ,中位数为
,中位数为![]() (3)140人
(3)140人
【解析】
(1)由题得![]() ,解方程即得解;(2)利用频率分布直方图中平均数和中位数的计算公式估计这200名学生的平均分和中位数;(3)分别计算每一段的人数即得解.
,解方程即得解;(2)利用频率分布直方图中平均数和中位数的计算公式估计这200名学生的平均分和中位数;(3)分别计算每一段的人数即得解.
(1)由![]() ,解得
,解得![]() .
.
(2)频率分布直方图中每一个小矩形的面积乘以底边中点的横坐标之和即为平均数,即估计平均数为![]() 。
。
设中位数为![]() ,则
,则![]() 解得
解得![]()
![]()
(3)由频率分布直方图可求出这200名学生的数学成绩在![]() ,
,![]() ,
,![]() 的分别有60人,40人,10人,按照表中给的比例,则英语成绩在
的分别有60人,40人,10人,按照表中给的比例,则英语成绩在![]() ,
,![]() ,
,![]() 的分别有50人,80人,10人,
的分别有50人,80人,10人,
所以英语成绩在![]() 的有140人。
的有140人。
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数f(x)=sin(2x+φ)+
 cos(2x+φ)(0<φ<π)图象向左平移
cos(2x+φ)(0<φ<π)图象向左平移  个单位后,得到函数的图象关于点(
个单位后,得到函数的图象关于点(  ,0)对称,则函数g(x)=cos(x+φ)在[﹣
,0)对称,则函数g(x)=cos(x+φ)在[﹣  ,
,  ]上的最小值是( )
]上的最小值是( )
A.﹣
B.﹣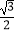
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设甲、乙、丙三个乒乓球协会分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为
 ,
, ,
, ,乙协会编号为
,乙协会编号为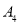 ,丙协会编号分别为
,丙协会编号分别为 ,
, ,若从这6名运动员中随机抽取2名参加双打比赛.
,若从这6名运动员中随机抽取2名参加双打比赛.(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
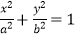 (a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
(a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
A.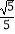
B.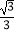
C.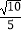
D.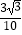
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣1﹣ax(a>1)在[0,a]上的最小值为f(x0),且x0<2,则实数a的取值范围是( )
A.(1,2)
B.(1,e)
C.(2,e)
D.( ,+∞)
,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司新上一条生产线,为保证新的生产线正常工作,需对该生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数
 ,标准差
,标准差 ,绘制如图所示的频率分布直方图,以频率值作为概率估值。
,绘制如图所示的频率分布直方图,以频率值作为概率估值。
(1)从该生产线加工的产品中任意抽取一件,记其数据为
 ,依据以下不等式评判(
,依据以下不等式评判( 表示对应事件的概率)
表示对应事件的概率)①

②

③

评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线,试判断该生产线是否需要检修;
(2)将数据不在
 内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为
内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为 ,求
,求 的分布列与数学期望
的分布列与数学期望 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 为常数.
为常数.(1)若
 ,求函数
,求函数 的极值;
的极值;(2)若函数
 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
相关试题

