【题目】已知椭圆 ![]() (a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
(a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:设椭圆的左、右焦点分别为F1(﹣c,0),F2(c,0),
由x=﹣c,代入椭圆方程可得y=± ![]() ,
,
可设A(﹣c, ![]() ),C(x,y),
),C(x,y),
由△ABF2的面积是△BCF2的面积的2倍,
可得 ![]() =2
=2 ![]() ,
,
即有(2c,﹣ ![]() )=2(x﹣c,y),
)=2(x﹣c,y),
即2c=2x﹣2c,﹣ ![]() =2y,
=2y,
可得x=2c,y=﹣ ![]() ,
,
代入椭圆方程可得, ![]() +
+ ![]() =1,
=1,
由e= ![]() ,b2=a2﹣c2 ,
,b2=a2﹣c2 ,
即有4e2+ ![]() ﹣
﹣ ![]() e2=1,
e2=1,
解得e= ![]() .
.
故选:A.
设椭圆的左、右焦点分别为F1(﹣c,0),F2(c,0),设x=﹣c,代入椭圆方程,求得A的坐标,设出C(x,y),由△ABF2的面积是△BCF2的面积的2倍,可得 ![]() =2
=2 ![]() ,运用向量的坐标运算可得x,y,代入椭圆方程,运用离心率公式,解方程即可得到所求值.
,运用向量的坐标运算可得x,y,代入椭圆方程,运用离心率公式,解方程即可得到所求值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称函数
成立,则称函数 是
是 上的有界函数,其中
上的有界函数,其中 称为函数的上界.已知函数
称为函数的上界.已知函数 .
.(1)当
 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;(2)若函数
 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围;
的取值范围;(3)若
 ,函数
,函数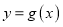 在
在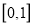 上的上界是
上的上界是 ,求
,求 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数f(x)=sin(2x+φ)+
 cos(2x+φ)(0<φ<π)图象向左平移
cos(2x+φ)(0<φ<π)图象向左平移  个单位后,得到函数的图象关于点(
个单位后,得到函数的图象关于点(  ,0)对称,则函数g(x)=cos(x+φ)在[﹣
,0)对称,则函数g(x)=cos(x+φ)在[﹣  ,
,  ]上的最小值是( )
]上的最小值是( )
A.﹣
B.﹣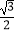
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设甲、乙、丙三个乒乓球协会分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为
 ,
, ,
, ,乙协会编号为
,乙协会编号为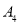 ,丙协会编号分别为
,丙协会编号分别为 ,
, ,若从这6名运动员中随机抽取2名参加双打比赛.
,若从这6名运动员中随机抽取2名参加双打比赛.(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是
 .
.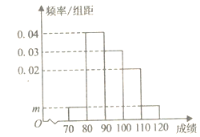
(1)求图中m的值;
(2)根据频率分布直方图,估计这200名学生的平均分(同一组中的数据用该组区间的中间值作代表)和中位数(四舍五入取整数);
(3)若这200名学生的数学成绩中,某些分数段的人数x与英语成绩相应分数段的人数y之比如下表所示,求英语成绩在
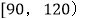 的人数.
的人数.分数段
[70,80)
[80,90)
[90,100)
[100,110)
[110,120)
x:y
1:2
2:1
6:5
1:2
1:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣1﹣ax(a>1)在[0,a]上的最小值为f(x0),且x0<2,则实数a的取值范围是( )
A.(1,2)
B.(1,e)
C.(2,e)
D.( ,+∞)
,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司新上一条生产线,为保证新的生产线正常工作,需对该生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数
 ,标准差
,标准差 ,绘制如图所示的频率分布直方图,以频率值作为概率估值。
,绘制如图所示的频率分布直方图,以频率值作为概率估值。
(1)从该生产线加工的产品中任意抽取一件,记其数据为
 ,依据以下不等式评判(
,依据以下不等式评判( 表示对应事件的概率)
表示对应事件的概率)①

②

③

评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线,试判断该生产线是否需要检修;
(2)将数据不在
 内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为
内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为 ,求
,求 的分布列与数学期望
的分布列与数学期望 。
。
相关试题

