【题目】已知:以点![]() (
(![]() )为圆心的圆与
)为圆心的圆与![]() 轴交
轴交
于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线![]() 与圆C交于点M, N,若OM = ON,求圆C的方程.
与圆C交于点M, N,若OM = ON,求圆C的方程.
参考答案:
【答案】(1)根据条件写成圆的方程,求出点A,B的坐标,进而写出△OAB的面积即可得证;
(2)![]()
【解析】试题分析:(1)设出圆C的方程,求得A、B的坐标,再根据S△AOB=![]() OAOB,计算可得结论.
OAOB,计算可得结论.
(2)设MN的中点为H,则CH⊥MN,根据C、H、O三点共线,KMN=﹣2,由直线OC的斜率![]() ,求得t的值,可得所求的圆C的方程.
,求得t的值,可得所求的圆C的方程.
试题解析:
(1)![]() ,
,![]() .
.
设圆![]() 的方程是
的方程是 ![]()
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]()
![]() ,即:
,即:![]() 的面积为定值.
的面积为定值.
(2)![]()
![]() 垂直平分线段
垂直平分线段![]() .
.
![]() ,
,![]() 直线
直线![]() 的方程是
的方程是![]() .
.
![]() ,解得:
,解得:![]()
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() ,圆
,圆![]() 与直线
与直线![]() 相交于两点.
相交于两点.
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() 圆
圆![]() 与直线
与直线![]() 不相交,
不相交,![]() 不符合题意舍去.
不符合题意舍去.
![]() 圆
圆![]() 的方程为
的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程
 ,变量
,变量 增加一个单位时,
增加一个单位时, 平均增加5个单位;③线性回归方程
平均增加5个单位;③线性回归方程 必过
必过 ;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )
;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )A.0 B.1 C. 2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论正确的是
①在某项测量中,测量结果
 服从正态分布
服从正态分布 .若
.若 在
在 内取值的概率为0.35,则
内取值的概率为0.35,则 在
在 内取值的概率为0.7;
内取值的概率为0.7;②以模型
 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设 ,其变换后得到线性回归方程
,其变换后得到线性回归方程 ,则
,则 ;
;③已知命题“若函数
 在
在 上是增函数,则
上是增函数,则 ”的逆否命题是“若
”的逆否命题是“若 ,则函数
,则函数 在
在 上是减函数”是真命题;
上是减函数”是真命题;④设常数
 ,则不等式
,则不等式 对
对 恒成立的充要条件是
恒成立的充要条件是 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分别直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间
 的有8人.
的有8人.
(I)求直方图中
 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间 的人数;
的人数;(II)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了了解高一新生男生得到体能状况,从高一新生中抽取若干名男生进行铅球测试,把所得数据(精确到0.1米)进行整理后,分成6组画出频率分布直方图的一部分(如下图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
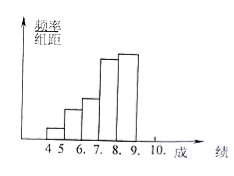
(1)请将频率分布直方图补充完整;
(2)该校参加这次铅球测试的男生有多少人?
(3)若成绩在8.0米以上(含8.0米)的为合格,试求这次铅球测试的成绩的合格率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图(如图所示),已知图中从左到右前三个小组的频率分别时0.1,0.3,0.4,第一小组的频数为5.
(1)求第四小组的频率?
(2)问参加这次测试的学生人数是多少?
(3)问在这次测试中,学生跳绳次数的中位数落在第几小组内?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
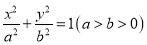 的左、右焦点分别为
的左、右焦点分别为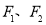 ,
,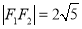 ,点
,点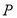 在椭圆上,
在椭圆上,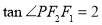 ,且
,且 的面积为4.
的面积为4.(1)求椭圆的方程;
(2)点
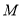 是椭圆上任意一点,
是椭圆上任意一点,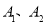 分别是椭圆的左、右顶点,直线
分别是椭圆的左、右顶点,直线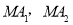 与直线
与直线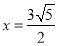 分别交于
分别交于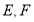 两点,试证:以
两点,试证:以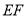 为直径的圆交
为直径的圆交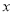 轴于定点,并求该定点的坐标.
轴于定点,并求该定点的坐标.
相关试题

