【题目】已知![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆上,
在椭圆上,![]() ,且
,且![]() 的面积为4.
的面积为4.
(1)求椭圆的方程;
(2)点![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 分别是椭圆的左、右顶点,直线
分别是椭圆的左、右顶点,直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点,试证:以
两点,试证:以![]() 为直径的圆交
为直径的圆交![]() 轴于定点,并求该定点的坐标.
轴于定点,并求该定点的坐标.
参考答案:
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,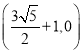 或
或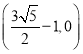 .
.
【解析】
试题分析:(1)由三角形的面积得![]() ,由余弦定理得
,由余弦定理得![]() ,结合椭圆的定义可得椭圆的标准方程;(2)求出
,结合椭圆的定义可得椭圆的标准方程;(2)求出![]() 、
、![]() 的坐标,设
的坐标,设![]() ,写出
,写出![]() ,
,![]() 的方程,并求出其与
的方程,并求出其与![]() 的交点
的交点![]() 的坐标,再设以
的坐标,再设以![]() 为直径的圆交
为直径的圆交![]() 轴于点
轴于点![]() ,则
,则![]() ,从而
,从而![]() ,可解出
,可解出![]() ,从而问题得以解决.
,从而问题得以解决.
试题解析:(1)因为![]() ,所以
,所以![]() ,
,![]() .
.
由题意得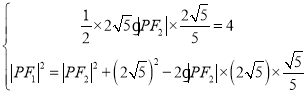 ,解得
,解得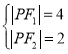 .
.
从而![]() ,结合
,结合![]() ,得
,得![]() ,
,
故椭圆的方程为![]() .
.
(2)由(1)得![]() ,
,![]() ,
,
设![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
它与直线![]() 的交点的坐标为
的交点的坐标为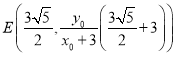 ,
,
直线![]() 的方程为
的方程为![]() ,它与直线
,它与直线![]() 的交点的坐标为
的交点的坐标为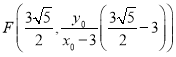 ,
,
再设以![]() 为直径的圆交
为直径的圆交![]() 轴于点
轴于点![]() ,则
,则![]() ,从而
,从而![]() ,即
,即
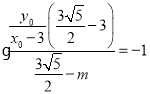 ,即
,即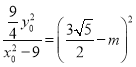 ,解得
,解得![]() .
.
故以![]() 为直径的圆交
为直径的圆交![]() 轴于定点,该定点的坐标为
轴于定点,该定点的坐标为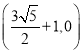 或
或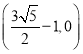 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:以点
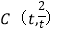 (
(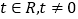 )为圆心的圆与
)为圆心的圆与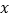 轴交
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线
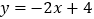 与圆C交于点M, N,若OM = ON,求圆C的方程.
与圆C交于点M, N,若OM = ON,求圆C的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了了解高一新生男生得到体能状况,从高一新生中抽取若干名男生进行铅球测试,把所得数据(精确到0.1米)进行整理后,分成6组画出频率分布直方图的一部分(如下图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
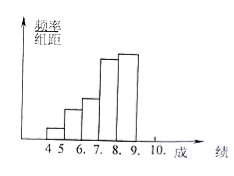
(1)请将频率分布直方图补充完整;
(2)该校参加这次铅球测试的男生有多少人?
(3)若成绩在8.0米以上(含8.0米)的为合格,试求这次铅球测试的成绩的合格率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图(如图所示),已知图中从左到右前三个小组的频率分别时0.1,0.3,0.4,第一小组的频数为5.
(1)求第四小组的频率?
(2)问参加这次测试的学生人数是多少?
(3)问在这次测试中,学生跳绳次数的中位数落在第几小组内?

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)设函数
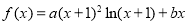 ,其中
,其中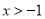 ,曲线
,曲线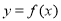 过点
过点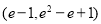 ,且在点
,且在点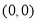 处的切线方程为
处的切线方程为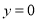 .
.(I)求
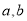 的值;
的值;(II)证明:当
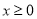 时,
时,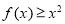 ;
;(III)若当
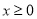 时,
时,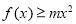 恒成立,求实数
恒成立,求实数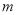 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用
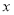 表示.
表示.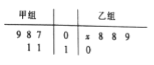
(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求
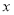 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
相关试题

