【题目】在直角坐标系xoy中,直线l经过点P(﹣1,0),其倾斜角为α,在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为ρ2﹣6ρcosθ+1=0. (Ⅰ)若直线l与曲线C有公共点,求α的取值范围;
(Ⅱ)设M(x,y)为曲线C上任意一点,求x+y的取值范围.
参考答案:
【答案】解:(Ⅰ)∵曲线C的极坐标方程为ρ2﹣6ρcosθ+1=0,∴曲线C的直角坐标方程为x2+y2﹣6x+1=0 ∵直线l经过点P(﹣1,0),其倾斜角为α,∴直线l的参数方程为 ![]() (t为参数)
(t为参数)
将 ![]() ,代入x2+y2﹣6x+1=0整理得t2﹣8tcosα+8=0
,代入x2+y2﹣6x+1=0整理得t2﹣8tcosα+8=0
∵直线l与曲线C有公共点,∴△=64cos2α﹣32≥0即 ![]() 或
或 ![]()
∵α∈[0,π)∴α的取值范围是 ![]()
(Ⅱ)曲线C的直角坐标方程为x2+y2﹣6x+1=0可化为(x﹣3)2+y2=8
其参数方程为 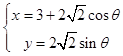 (θ为参数)
(θ为参数)
∵M(x,y)为曲线C上任意一点,∴ ![]()
∴x+y的取值范围是[﹣1,7].
【解析】(Ⅰ)由直线l经过点P(﹣1,0),且倾斜角为α,可得直线l的参数方程,利用互化公式可得C的直角坐标方程.由直线l与曲线C有公共点,可得△=64cos2α﹣32≥0,解出即可得出的取值范围; (Ⅱ)设M(x,y)为曲线C上任意一点,利用参数方程为 ![]() (θ为参数),结合三角函数知识求x+y的取值范围.
(θ为参数),结合三角函数知识求x+y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. (Ⅰ)求证:EF⊥平面PAC;
(Ⅱ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求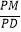 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,曲线Γ由曲线C1:
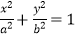 (a>b>0,y≤0)和曲线C2:
(a>b>0,y≤0)和曲线C2: 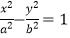 (a>0,b>0,y>0)组成,其中点F1 , F2为曲线C1所在圆锥曲线的焦点,点F3 , F4为曲线C2所在圆锥曲线的焦点,
(a>0,b>0,y>0)组成,其中点F1 , F2为曲线C1所在圆锥曲线的焦点,点F3 , F4为曲线C2所在圆锥曲线的焦点,
(Ⅰ)若F2(2,0),F3(﹣6,0),求曲线Γ的方程;
(Ⅱ)如图,作直线l平行于曲线C2的渐近线,交曲线C1于点A、B,求证:弦AB的中点M必在曲线C2的另一条渐近线上;
(Ⅲ)对于(Ⅰ)中的曲线Γ,若直线l1过点F4交曲线C1于点C、D,求△CDF1面积的最大值.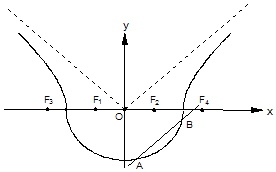
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=
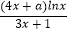 ,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)求a的值;
,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)求a的值;
(Ⅱ)若对于任意的x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的取值范围;
(Ⅲ)求证:ln(4n+1)≤16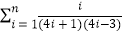 (n∈N*).
(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,a2n﹣1+a2n<0”的条件.(填“充要条件、充分不必要条件、必要不充分条件、即不充分也不必要条件”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】设命题
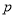 :
: 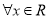 ,函数
,函数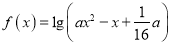 有意义;命题
有意义;命题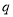 :
: 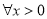 ,不等式
,不等式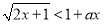 恒成立,如果命题“
恒成立,如果命题“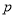 或
或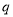 ”为真命题,命题“
”为真命题,命题“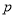 且
且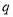 ”为假命题,求实数
”为假命题,求实数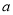 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若n=4时,则输出的结果为 .

相关试题

