【题目】已知直线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 点,动圆
点,动圆![]() 与直线
与直线![]() 相切,并且与圆
相切,并且与圆![]() 相外切,
相外切,
(1)求动圆的圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若过原点且倾斜角为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,问是否存在以
两点,问是否存在以![]() 为直径的圆经过点
为直径的圆经过点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() (
(![]() )(2)故不存在以
)(2)故不存在以![]() 为直径的圆恰好过点
为直径的圆恰好过点![]()
【解析】试题分析:(1)设出动圆圆心坐标,由动圆圆心到切线的距离等于动圆与定圆的圆心距减定圆的半径列式求解动圆圆心的轨迹方程;
(2)求出过原点且倾斜角为![]() 的直线方程,和曲线C联立后利用根与系数关系得到M,N的横纵坐标的和与积,由
的直线方程,和曲线C联立后利用根与系数关系得到M,N的横纵坐标的和与积,由![]() ,得
,得![]() 列式求解m的值,结合m的范围说明不存在以MN为直径的圆过点A.
列式求解m的值,结合m的范围说明不存在以MN为直径的圆过点A.
试题解析:
(1)设动圆圆心为![]() ,则
,则![]() ,化简得
,化简得![]() (
(![]() ),这就是动圆圆心的轨迹
),这就是动圆圆心的轨迹![]() 的方程.
的方程.
(2)直线![]() 的方程为
的方程为![]() ,代入曲线
,代入曲线![]() 的方程得
的方程得![]()
显然![]() .
.
设![]() ,
, ![]() ,则
,则![]()
![]() ,
, ![]()
![]() ,
,
而![]()
若以![]() 为直径的圆过点
为直径的圆过点![]() ,则
,则![]() ,
,
∴![]() 由此得
由此得![]()
∴![]() ,即
,即![]() .
.
解得![]() >-2
>-2
故不存在以![]() 为直径的圆过点
为直径的圆过点![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=3sin(2x+
 )的图象为C,关于函数f(x)及其图象的判断如下: ①图象C关于点(
)的图象为C,关于函数f(x)及其图象的判断如下: ①图象C关于点(  ,0)对称;
,0)对称;
②图象C关于直线x=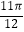 对称;
对称;
③由图象C向右平移 个单位长度可以得到y=3sin2x的图象;
个单位长度可以得到y=3sin2x的图象;
④函数f(x)在区间(﹣ ,
, 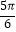 )内是减函数;
)内是减函数;
⑤函数|f(x)+1|的最小正周期为 .
.
其中正确的结论序号是 . (把你认为正确的结论序号都填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
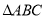 的三个顶点
的三个顶点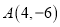 ,
, 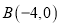 ,
, 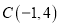 ,求:
,求:(1)
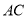 边上的高
边上的高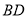 所在直线的方程;
所在直线的方程;(2)
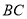 的垂直平分线
的垂直平分线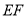 所在直线的方程;
所在直线的方程;(3)
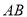 边的中线的方程.
边的中线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.
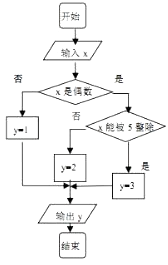
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据: 甲的频数统计表(部分)运行次数
输出y=1的频数
输出y=2的频数
输出y=3的频数
50
24
19
7
…
…
…
…
2000
1027
776
197
乙的频数统计表(部分)
运行次数
输出y=1的频数
输出y=2的频数
输出y=3的频数
50
26
11
13
…
…
…
…
2000
1051
396
553
当n=2000时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;
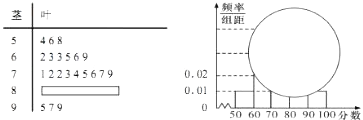
(1)求分数在[50,60)的频率及全班的人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)根据频率分布直方图,估计该班数学成绩的平均数与中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
 )在某一周期内的图象时,列表并填入了部分数据,如下表:
)在某一周期内的图象时,列表并填入了部分数据,如下表: ωx+φ
0

π
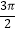
2π
x

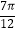
Asin(ωx+φ)
3
0
(1)请将上表空格中的数据在答卷的相应位置上,并求函数f(x)的解析式;
(2)若y=f(x)的图象上所有点向左平移 个单位后对应的函数为g(x),求当x∈[﹣
个单位后对应的函数为g(x),求当x∈[﹣  ,
,  ]时,函数y=g(x)的值域.
]时,函数y=g(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
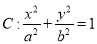 (
(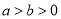 ),的两个焦点
),的两个焦点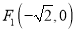 ,
, 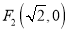 ,点
,点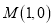 在此椭圆上.
在此椭圆上.(1)求椭圆
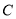 的方程;
的方程;(2)过点
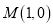 的直线
的直线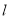 与椭圆
与椭圆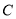 相交于
相交于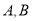 两点,设点
两点,设点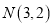 ,记直线
,记直线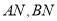 的斜率分别为
的斜率分别为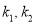 ,求证:
,求证: 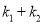 为定值.
为定值.
相关试题

