【题目】已知椭圆![]() (
(![]() ),的两个焦点
),的两个焦点![]() ,
, ![]() ,点
,点![]() 在此椭圆上.
在此椭圆上.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证: ![]() 为定值.
为定值.
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)依题意, ![]() ,利用点
,利用点![]() 与椭圆短轴的两个端点的连线相互垂直,可得
与椭圆短轴的两个端点的连线相互垂直,可得![]() ,从而可得椭圆的方程;
,从而可得椭圆的方程;
(2)①当直线![]() 的斜率不存在时,求出
的斜率不存在时,求出![]() 的坐标,进而可得直线
的坐标,进而可得直线![]() 的斜率,即可求得结论;②当直线
的斜率,即可求得结论;②当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的方程为:
的方程为: ![]() ,代入
,代入![]() ,利用韦达定理及斜率公式可得结论.
,利用韦达定理及斜率公式可得结论.
试题解析:(1)根据焦点坐标得: ![]() ,而点
,而点![]() 与椭圆短轴的两个端点的连线相互垂直,根据椭圆的对称性故有
与椭圆短轴的两个端点的连线相互垂直,根据椭圆的对称性故有![]() ;所以
;所以![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)①当直线的斜率不存在时,由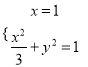 ,解得
,解得![]() ,不妨设
,不妨设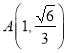 ,
, 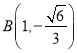 ,则
,则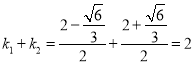 为定值。
为定值。
②当直线l的斜率存在时,设直线l的方程为![]() ,将
,将![]() 代入
代入![]() 整理化简得:
整理化简得: ![]() 。
。
设![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]()
![]()
![]()
![]() ,
,
综上![]() 为常数2.
为常数2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 (
( )与
)与 轴交于
轴交于 点,动圆
点,动圆 与直线
与直线 相切,并且与圆
相切,并且与圆 相外切,
相外切,(1)求动圆的圆心
 的轨迹
的轨迹 的方程;
的方程;(2)若过原点且倾斜角为
 的直线与曲线
的直线与曲线 交于
交于 两点,问是否存在以
两点,问是否存在以 为直径的圆经过点
为直径的圆经过点 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;
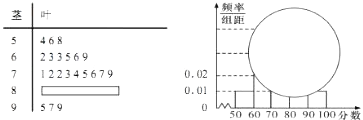
(1)求分数在[50,60)的频率及全班的人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)根据频率分布直方图,估计该班数学成绩的平均数与中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
 )在某一周期内的图象时,列表并填入了部分数据,如下表:
)在某一周期内的图象时,列表并填入了部分数据,如下表: ωx+φ
0

π
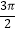
2π
x

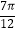
Asin(ωx+φ)
3
0
(1)请将上表空格中的数据在答卷的相应位置上,并求函数f(x)的解析式;
(2)若y=f(x)的图象上所有点向左平移 个单位后对应的函数为g(x),求当x∈[﹣
个单位后对应的函数为g(x),求当x∈[﹣  ,
,  ]时,函数y=g(x)的值域.
]时,函数y=g(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
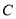 过
过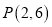 ,
, 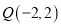 两点,且圆心
两点,且圆心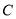 在直线
在直线 上.
上.(1)求圆
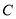 的方程;
的方程;(2)若直线
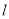 过点
过点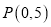 且被圆
且被圆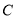 截得的线段长为
截得的线段长为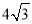 ,求
,求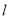 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
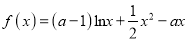 (
(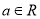 )
)(1)讨论
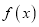 的单调性;
的单调性;(2)设
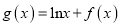 ,若
,若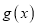 有两个极值点
有两个极值点 ,且不等式
,且不等式 恒成立,求实数
恒成立,求实数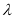 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 为圆
为圆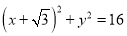 ,
, 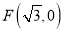 ,
, 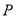 是圆上的动点,线段
是圆上的动点,线段 的垂直平分线交
的垂直平分线交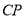 于点
于点 .
.(1)求点
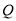 的轨迹
的轨迹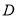 的方程;
的方程;(2)设
 ,
, 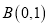 ,过点
,过点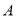 的直线
的直线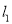 与曲线
与曲线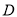 交于点
交于点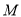 (异于点
(异于点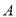 ),过点
),过点 的直线
的直线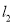 与曲线
与曲线 交于点
交于点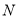 ,直线
,直线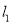 与
与 倾斜角互补.
倾斜角互补.①直线
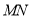 的斜率是否为定值?若是,求出该定值;若不是,说明理由;
的斜率是否为定值?若是,求出该定值;若不是,说明理由;②设
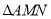 与
与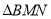 的面积之和为
的面积之和为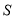 ,求
,求 的取值范围.
的取值范围.
相关试题

