【题目】某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题; 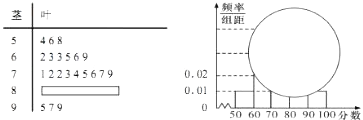
(1)求分数在[50,60)的频率及全班的人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)根据频率分布直方图,估计该班数学成绩的平均数与中位数.
参考答案:
【答案】
(1)解:分数在[50,60)的频率为0.01×10=0.1,
由茎叶图知:分数在[50,60)之间的频数为3,所以全班人数为30
(2)解:分数在[80,90)之间的频数为30﹣3﹣6﹣9﹣3=9,
频率分布直方图中[80,90)间的矩形的高为9÷30÷10=0.03
(3)解: ![]() =55×0.1+65×
=55×0.1+65× ![]() +75×
+75× ![]() +85×
+85× ![]() +95×
+95× ![]() =76,
=76,
所以该班数学成绩的平均分数估计为76分
【解析】(Ⅰ)根据分数在[50,60)的频率为0.01×10,和由茎叶图知分数在[50,60)之间的频数为3,得到全班人数.(2)分数在[80,90)之间的频数为30﹣3﹣6﹣9﹣3,做出频率,根据小长方形的高是频率比组距,得到结果.(3)用各矩形中点的横坐标乘以本段的频率作和.
【考点精析】根据题目的已知条件,利用频率分布直方图和平均数、中位数、众数的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
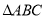 的三个顶点
的三个顶点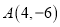 ,
, 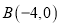 ,
, 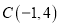 ,求:
,求:(1)
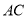 边上的高
边上的高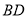 所在直线的方程;
所在直线的方程;(2)
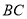 的垂直平分线
的垂直平分线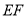 所在直线的方程;
所在直线的方程;(3)
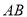 边的中线的方程.
边的中线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.
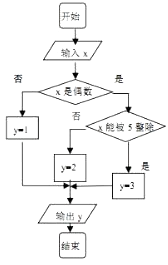
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据: 甲的频数统计表(部分)运行次数
输出y=1的频数
输出y=2的频数
输出y=3的频数
50
24
19
7
…
…
…
…
2000
1027
776
197
乙的频数统计表(部分)
运行次数
输出y=1的频数
输出y=2的频数
输出y=3的频数
50
26
11
13
…
…
…
…
2000
1051
396
553
当n=2000时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 (
( )与
)与 轴交于
轴交于 点,动圆
点,动圆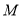 与直线
与直线 相切,并且与圆
相切,并且与圆 相外切,
相外切,(1)求动圆的圆心
 的轨迹
的轨迹 的方程;
的方程;(2)若过原点且倾斜角为
 的直线与曲线
的直线与曲线 交于
交于 两点,问是否存在以
两点,问是否存在以 为直径的圆经过点
为直径的圆经过点 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
 )在某一周期内的图象时,列表并填入了部分数据,如下表:
)在某一周期内的图象时,列表并填入了部分数据,如下表: ωx+φ
0

π
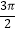
2π
x

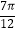
Asin(ωx+φ)
3
0
(1)请将上表空格中的数据在答卷的相应位置上,并求函数f(x)的解析式;
(2)若y=f(x)的图象上所有点向左平移 个单位后对应的函数为g(x),求当x∈[﹣
个单位后对应的函数为g(x),求当x∈[﹣  ,
,  ]时,函数y=g(x)的值域.
]时,函数y=g(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
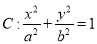 (
(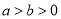 ),的两个焦点
),的两个焦点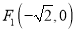 ,
, 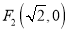 ,点
,点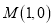 在此椭圆上.
在此椭圆上.(1)求椭圆
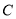 的方程;
的方程;(2)过点
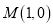 的直线
的直线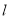 与椭圆
与椭圆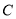 相交于
相交于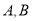 两点,设点
两点,设点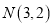 ,记直线
,记直线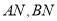 的斜率分别为
的斜率分别为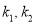 ,求证:
,求证: 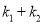 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
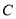 过
过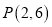 ,
, 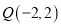 两点,且圆心
两点,且圆心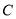 在直线
在直线 上.
上.(1)求圆
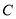 的方程;
的方程;(2)若直线
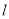 过点
过点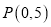 且被圆
且被圆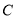 截得的线段长为
截得的线段长为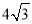 ,求
,求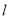 的方程.
的方程.
相关试题

