【题目】如图,已知离心率为 ![]() 的椭圆
的椭圆 ![]() 过点M(2,1),O为坐标原点,平行于OM的直线i交椭圆C于不同的两点A、B.
过点M(2,1),O为坐标原点,平行于OM的直线i交椭圆C于不同的两点A、B. 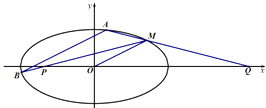
(1)求椭圆C的方程;
(2)记直线MB、MA与x轴的交点分别为P、Q,若MP斜率为k1 , MQ斜率为k2 , 求k1+k2 .
参考答案:
【答案】
(1)解:设椭圆C的方程为: ![]() .
.
由题意得:  ,
,
把①代入②得:a2=4b2④.
联立③④得:a2=8,b2=2.
∴椭圆方程为 ![]()
(2)解:∵M(2,1),∴kOM= ![]()
又∵直线l∥OM,可设l:y= ![]() x+m,将式子代入椭圆C得:x2+4(
x+m,将式子代入椭圆C得:x2+4( ![]() x+m)2﹣8=0,
x+m)2﹣8=0,
整理得:x2+2mx+2m2﹣4=0.
设A(x1,y1),B(x2,y2),则x1+x2=﹣2m,x1x2=2m2﹣4.
设直线MA、MB的斜率分别为k1、k2,则k1= ![]() ,k2=
,k2= ![]() .
.
事实上,k1+k2= ![]() +
+ ![]()
= ![]() =1+m(
=1+m( ![]() +
+ ![]() )
)
=1+m ![]()
=1+m ![]()
=1﹣ ![]()
=0.
k1+k2的值为0
【解析】(1)由给出的椭圆的离心率、椭圆过定点M(2,1)及隐含条件a2=b2+c2列方程组可求a2 , b2 , 则椭圆方程可求;(2)设出直线l的方程,设出A,B两点的坐标,把直线和椭圆联立后可求A,B两点的横坐标的和与积,把直线MA,MB的斜率k1、k2分别用A,B两点的坐标表示,把纵坐标转化为横坐标后,则k1+k2仅含A,B两点的横坐标的和与积,化简整理即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P﹣ABCD,底面四边形ABCD为菱形,AB=2,BD=2
 ,M,N分别是线段PA,PC的中点. (Ⅰ)求证:MN∥平面ABCD;
,M,N分别是线段PA,PC的中点. (Ⅰ)求证:MN∥平面ABCD;
(Ⅱ)求异面直线MN与BC所成角的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线x2=2py(p>0)与直线2x﹣y+1=0交于A,B两点,
 ,点M在抛物线上,MA⊥MB.
,点M在抛物线上,MA⊥MB. 
(1)求p的值;
(2)求点M的横坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={(x,y)|y=a},集合B={(x,y)|y=bx+1,b>0,b≠1},若集合A∩B≠,则实数a的取值范围是( )
A.(﹣∞,1)
B.(﹣∞,1]
C.[1,+∞)
D.(1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=
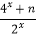 是奇函数,f(x)=log4(4x+1)﹣mx是偶函数.
是奇函数,f(x)=log4(4x+1)﹣mx是偶函数.
(1)求m+n的值;
(2)设h(x)=f(x)+ x,若g(x)>h[log4(2a+1)]对任意x≥1恒成立,求实数a的取值范围.
x,若g(x)>h[log4(2a+1)]对任意x≥1恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两个正根,求m的取值范围.
(2)若方程有两根,其中一根在区间(﹣1,0)内,另一根在区间(1,3)内,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲,乙,丙,丁四位同学课余参加巴蜀爱心社和巴蜀文学风的活动,每人参加且只能参加一个社团的活动,并且参加每个社团都是等可能的.
(1)求巴蜀爱心社和巴蜀文学风都至少有1人参加的概率;
(2)求甲,乙在同一个社团,丙,丁不在同一个社团的概率.
相关试题

