【题目】如图,已知四棱锥P﹣ABCD,底面四边形ABCD为菱形,AB=2,BD=2 ![]() ,M,N分别是线段PA,PC的中点. (Ⅰ)求证:MN∥平面ABCD;
,M,N分别是线段PA,PC的中点. (Ⅰ)求证:MN∥平面ABCD;
(Ⅱ)求异面直线MN与BC所成角的大小.
参考答案:
【答案】(Ⅰ)证明:连结AC,交BD于点O, 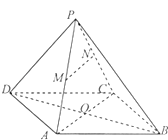
∵M,N分别是PA,PC的中点,∴MN∥AC,
∵MN平面ABCD,AC平面ABCD,
∴MN∥平面ABCD.
(Ⅱ)解:由(Ⅰ)知∠ACB是异面直线MN与BC所成的角或其补角,
∵四边形ABCD是菱形,AB=2,BO= ![]() ,
,
∴∠OCB=60°,
∴异面直线MN与BC所成的角为60°.
【解析】(Ⅰ)连结AC,交BD于点O,由已知得MN∥AC,由此能证明MN∥平面ABCD.(Ⅱ)由已知得∠ACB是异面直线MN与BC所成的角或其补角,由此能求出异面直线MN与BC所成的角.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系,以及对直线与平面平行的判定的理解,了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
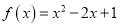 ,
,  .
.(1)求函数
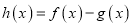 的极值;
的极值;(2)当
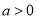 时,若存在实数
时,若存在实数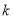 ,
, 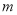 使得不等式
使得不等式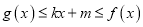 恒成立,求实数
恒成立,求实数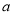 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若采用随机模拟的方法估计某运动员射击击中目标的概率.先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
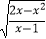 的定义域是( )
的定义域是( )
A.(0,2)
B.[0,2]
C.(0,1)∪(1,2)
D.[0,1)∪(1,2] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线x2=2py(p>0)与直线2x﹣y+1=0交于A,B两点,
 ,点M在抛物线上,MA⊥MB.
,点M在抛物线上,MA⊥MB. 
(1)求p的值;
(2)求点M的横坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={(x,y)|y=a},集合B={(x,y)|y=bx+1,b>0,b≠1},若集合A∩B≠,则实数a的取值范围是( )
A.(﹣∞,1)
B.(﹣∞,1]
C.[1,+∞)
D.(1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知离心率为
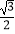 的椭圆
的椭圆 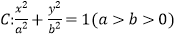 过点M(2,1),O为坐标原点,平行于OM的直线i交椭圆C于不同的两点A、B.
过点M(2,1),O为坐标原点,平行于OM的直线i交椭圆C于不同的两点A、B. 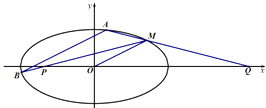
(1)求椭圆C的方程;
(2)记直线MB、MA与x轴的交点分别为P、Q,若MP斜率为k1 , MQ斜率为k2 , 求k1+k2 .
相关试题

