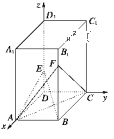
【题目】如图,在正四棱柱![]() 中,已知AB=2,
中,已知AB=2,![]() ,
,
E、F分别为![]() 、
、![]() 上的点,且
上的点,且![]() .
.

(1)求证:BE⊥平面ACF;
(2)求点E到平面ACF的距离.
参考答案:
【答案】(1)见解析(2)![]()
【解析】
分析:(1)以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴建立空间直角坐标系,写出要用的点的坐标,要证明线与面垂直,只需证明这条直线与平面上的两条直线垂直即可;(2)
轴建立空间直角坐标系,写出要用的点的坐标,要证明线与面垂直,只需证明这条直线与平面上的两条直线垂直即可;(2)![]() 为平面
为平面![]() 的一个法向量,向量
的一个法向量,向量![]() 在
在![]() 上的射影长即为
上的射影长即为![]() 到平面
到平面![]() 的距离,根据点到面的距离公式可得到结论.
的距离,根据点到面的距离公式可得到结论.
详解:(1)证明:以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立如图所示空间直角坐标系,则D(0,0,0)、A(2,0,0)、B(2,2,0)、C(0,2,0)、D1(0,0,5)、E(0,0,1)、F(2,2,4).
∴![]() =(-2,2,0)、
=(-2,2,0)、![]() =(0,2,4)、
=(0,2,4)、![]() =(-2,-2,1)、
=(-2,-2,1)、![]() =(-2,0,1).
=(-2,0,1).
∵![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,
=0,
∴BE⊥AC,BE⊥AF,且AC∩AF=A.
∴BE⊥平面ACF.
(2)由(1)知,![]() 为平面ACF的一个法向量,
为平面ACF的一个法向量,
∴点E到平面ACF的距离d=![]() =
=![]() .
.
故点E到平面ACF的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos
 ,g(x)=exf(x),其中e为自然对数的底数.
,g(x)=exf(x),其中e为自然对数的底数.
(1)求曲线y=g(x)在点(0,g(0))处的切线方程;
(2)若对任意 时,方程g(x)=xf(x)的解的个数,并说明理由.
时,方程g(x)=xf(x)的解的个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A=a1 , a2 , a3 , …,an , 其中ai∈R(1≤i≤n,n>2),l(A)表示和ai+aj(1≤i<j≤n)中所有不同值的个数.
(Ⅰ)设集合P=2,4,6,8,Q=2,4,8,16,分别求l(P)和l(Q);
(Ⅱ)若集合A=2,4,8,…,2n , 求证: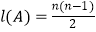 ;
;
(Ⅲ)l(A)是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1边长为1,下底面ABCD边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成角的余弦值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元.

(1)设∠ADC=α,试将运输总费用S(单位:元)表示为α的函数S(α),并写出自变量的取值范围;
(2)问中转站D建在何处时,运输总费用S最小?并求出最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,平面
中,平面 平面
平面 ;
;  ,
,  ,
,  ,
,  .
.(1)证明:
 平面
平面 ;
;(2)求直线
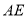 与平面
与平面 所成的角的正切值.
所成的角的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
(1)求证:FC∥平面EAD;
(2)求二面角A-FC-B的余弦值.

相关试题

