【题目】已知椭圆的焦点在x轴上,中心在坐标原点,离心率![]() ,椭圆上的点到左焦点的距离的最大值为
,椭圆上的点到左焦点的距离的最大值为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆的右焦点F作与坐标轴不垂直的直线l,交椭圆于A、B两点,设点![]() 是线段OF上的一个动点,且
是线段OF上的一个动点,且![]() ,求m的取值范围;
,求m的取值范围;
(3)设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C、B、N三点共线?若存在,求出定点N的坐标,若不存在,请说明理由;
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)定点
;(3)定点![]() ,证明过程见解析
,证明过程见解析
【解析】
(1)由椭圆上的点到左焦点的距离的最大值即![]() 和离心率
和离心率![]() ,求出
,求出![]() 和
和![]() ,再求出
,再求出![]() ,即可求出椭圆标准方程;
,即可求出椭圆标准方程;
(2)设直线方程![]() ,代入椭圆方程,并利用韦达定理求出
,代入椭圆方程,并利用韦达定理求出![]() 和
和![]() ,设
,设![]() 中点为
中点为![]() ,将
,将![]() 转化为
转化为![]() ,表示出
,表示出![]() ,即可得到
,即可得到![]() 的范围;
的范围;
(3)求出点![]() 坐标,再设点
坐标,再设点![]() ,由C、B、N三点共线得到
,由C、B、N三点共线得到![]() ,利用向量平行的坐标形式表示出
,利用向量平行的坐标形式表示出![]() ,再利用(2)中的韦达定理化简即可得到定点
,再利用(2)中的韦达定理化简即可得到定点![]() 的坐标.
的坐标.
(1)由题意,椭圆焦点在![]() 轴上,设椭圆方程
轴上,设椭圆方程![]() ,
,
则椭圆上的点到左焦点的距离的最大值即![]() ,
,
又![]() ,解得
,解得![]() ,
,![]() ,所以
,所以![]() ,
,
所以椭圆标准方程为:![]() .
.
(2)由题意,点![]() ,
,
因为点![]() 在线段
在线段![]() 上,所以
上,所以![]() ,
,
设过点![]() 的直线方程为
的直线方程为![]() ,
,
代入椭圆方程并整理得,![]() ,
,
设点![]() ,点
,点![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
设![]() 中点
中点![]() ,
,
由![]() ,可得
,可得![]() ,
,
所以![]() ,即
,即![]() ,
,
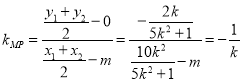 ,
,
整理得,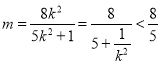 ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.
(3)由(2)知![]() ,点
,点![]() 和点
和点![]() 关于
关于![]() 轴对称,所以
轴对称,所以![]() ,
,
设点![]() ,则
,则![]() ,
,![]() ,
,
当C、B、N三点共线时,即![]() ,
,
所以![]() ,
,
整理得,![]() ,
,
由(2)知,![]() ,
,![]() ,
,![]() ,
,
所以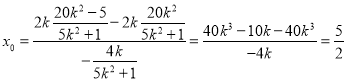 ,
,
所以定点![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
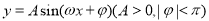 的一段图象如图所示.
的一段图象如图所示.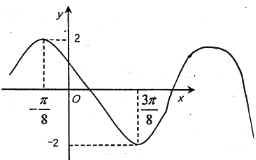
(1)求该函数的解析式;
(2)求该函数的单调增区间;
(3)该函数的图象可由
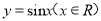 的图象经过怎样的平移和伸缩变换得到的?
的图象经过怎样的平移和伸缩变换得到的? -
科目: 来源: 题型:
查看答案和解析>>【题目】一半径为2米的水轮如图所示,水轮圆心
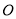 距离水面1米;已知水轮按逆时针做匀速转动,每3秒转一圈,如果当水轮上点
距离水面1米;已知水轮按逆时针做匀速转动,每3秒转一圈,如果当水轮上点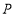 从水中浮现时(图中点
从水中浮现时(图中点 )开始计算时间.
)开始计算时间.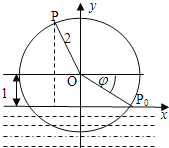
(1)试将点
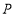 距离水面的高度
距离水面的高度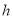 (单位:米)表示为时间
(单位:米)表示为时间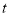 (单位:秒)的函数
(单位:秒)的函数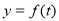 ;
;(2)点
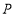 第一次到达最高点大约要多长时间?
第一次到达最高点大约要多长时间?(3)求
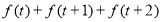 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,
, ,
, ,
, ,函数
,函数 ,
, 的最小正周期为
的最小正周期为 .
.(1)求
 的单调增区间;
的单调增区间;(2)方程
 ;在
;在 上有且只有一个解,求实数n的取值范围;
上有且只有一个解,求实数n的取值范围;(3)是否存在实数m满足对任意x1∈[-1,1],都存在x2∈R,使得
 +
+ +m(
+m( -
- )+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由.
)+1>f(x2)成立.若存在,求m的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月22日是第50个世界地球日,半个世纪以来,这一呼吁热爱地球环境的运动已经演变为席卷全球的绿色风暴,让越来越多的人认识到保护环境、珍惜自然对人类未来的重要性.今年,自然资源部地球日的主题是“珍爱美丽地球,守护自然资源”.某中学举办了以“珍爱美地球,守护自然资源”为主题的知识竞赛.赛后从该校高一和高二年级的参赛者中随机抽取100人,将他们的竞赛成绩分为7组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下频率分布表:

现规定,“竞赛成绩≥80分”为“优秀”“竞赛成绩<80分”为“非优秀”
(Ⅰ)请将下面的2×2列联表补充完整;
优秀
非优秀
合计
高一
50
高二
15
合计
100
(Ⅱ)判断是否有99%的把握认为“竞赛成绩与年级有关”?
附:独立性检验界值

-
科目: 来源: 题型:
查看答案和解析>>【题目】设
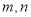 是两条不同的直线,
是两条不同的直线,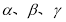 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:①若
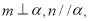 则
则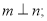
②若
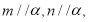 则
则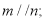
③若
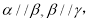 则
则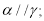
④若
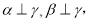 则
则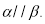
其中正确命题的序号是( )
A.①和③B.②和③C.②和④D.①和④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
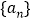 的前
的前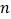 项和
项和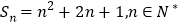 .
.(1)求数列
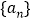 的通项公式;
的通项公式;(2)求数列
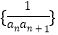 的前
的前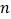 项和
项和 .
.
相关试题

