【题目】定义:对于实数![]() 和两定点
和两定点![]() ,在某图形上恰有
,在某图形上恰有![]() 个不同的点
个不同的点![]() ,使得
,使得![]() ,称该图形满足“
,称该图形满足“![]() 度契合”.若边长为4的正方形
度契合”.若边长为4的正方形![]() 中,
中,![]() ,且该正方形满足“4度契合”,则实数
,且该正方形满足“4度契合”,则实数![]() 的取值范围是__________.
的取值范围是__________.
参考答案:
【答案】![]() 或
或![]()
【解析】
分析:根据定义,分类讨论P点在四条边上的不同情况;转化成m的表达式后,利用二次函数求得m的范围;分析在四种情况下,哪个符合有4个解,即可得到m的取值。
详解:以AB为x轴,AD为y轴,A为原点建立平面直角坐标系。所以![]() 。因为P点位置不确定,所以分四种情况讨论:
。因为P点位置不确定,所以分四种情况讨论:
当P点在AB上时,设![]() ,
,![]()
所以![]()
所以
![]()
根据二次函数的图像可知,当![]() 时,有1个解
时,有1个解
当![]() 时,有2个解
时,有2个解
(2)当P点在BC上时,设![]() ,
,![]()
所以![]()
所以
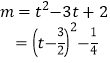
根据二次函数的图像可知,当![]() 时,有1个解
时,有1个解
当![]() 时,有2个解
时,有2个解
当![]() 时,有1个解
时,有1个解
(3)当P点在CD上时,设![]() ,
,![]()
所以![]()
所以
![]()
根据二次函数的图像可知,当![]() 时,有1个解
时,有1个解
当![]() 时,有2个解
时,有2个解
(4)当P点在AD上时,设![]() ,
,![]()
所以![]()
所以
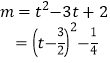
根据二次函数的图像可知,当![]() 时,有1个解
时,有1个解
当![]() 时,有2个解
时,有2个解
当![]() 时,有2个解
时,有2个解
由(1)可知,当![]() 时,有2个解。所以当
时,有2个解。所以当![]() 时,也有2个解
时,也有2个解
综上所述,当![]() 或
或![]() 有4个解,满足“
有4个解,满足“![]() 度契合”。
度契合”。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 ,则方程
,则方程 (
( 为正实数)的实数根最多有_____个
为正实数)的实数根最多有_____个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
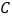 :
: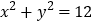 ,直线
,直线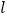 :
: ,圆
,圆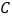 上的点
上的点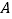 到直线
到直线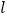 的距离小于2的概率为( )
的距离小于2的概率为( )A.
 B.
B.  C.
C. 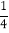 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知任意角
中,已知任意角 以坐标原点
以坐标原点 为顶点,
为顶点, 轴的非负半轴为始边,若终边经过点
轴的非负半轴为始边,若终边经过点 ,且
,且 ,定义:
,定义: ,称“
,称“ ”为“正余弦函数”,对于“正余弦函数
”为“正余弦函数”,对于“正余弦函数 ”,有同学得到以下性质:
”,有同学得到以下性质:①该函数的值域为
 ; ②该函数的图象关于原点对称;
; ②该函数的图象关于原点对称;③该函数的图象关于直线
 对称; ④该函数为周期函数,且最小正周期为
对称; ④该函数为周期函数,且最小正周期为 ;
;⑤该函数的递增区间为
 .
.其中正确的是__________.(填上所有正确性质的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,圆
中,圆 :
: 与
与 轴的正半轴交于点
轴的正半轴交于点 ,以点
,以点 为圆心的圆
为圆心的圆 :
: 与圆
与圆 交于
交于 ,
, 两点.
两点.(1)当
 时,求
时,求 的长;
的长;(2)当
 变化时,求
变化时,求 的最小值;
的最小值;(3)过点
 的直线
的直线 与圆A切于点
与圆A切于点 ,与圆
,与圆 分别交于点
分别交于点 ,
, ,若点
,若点 是
是 的中点,试求直线
的中点,试求直线 的方程.
的方程. 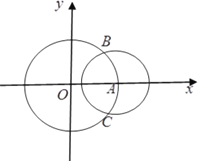
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有
 名学生参加学校组织的“数学竞赛集训队”选拔考试,现从中等可能抽出
名学生参加学校组织的“数学竞赛集训队”选拔考试,现从中等可能抽出 名学生的成绩作为样本,制成如图频率分布表:
名学生的成绩作为样本,制成如图频率分布表:分组
频数
频率

0.025

0.050

0.200
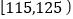
12
0.300

0.275

4

0.00
合计

1
(1)求
 的值,并根据题中信息估计总体平均数是多少?
的值,并根据题中信息估计总体平均数是多少?(2)若成绩不低于
 分的同学能参加“数学竞赛集训队”,试估计该校大约多少名学生能参加“数学竞赛集训队”?
分的同学能参加“数学竞赛集训队”,试估计该校大约多少名学生能参加“数学竞赛集训队”? -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2
 cos
cos ,直线l的参数方程为
,直线l的参数方程为 (t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.(1)求圆心的极坐标;
(2)求△PAB面积的最大值.
相关试题

