【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2![]() cos
cos![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(1)求圆心的极坐标;
(2)求△PAB面积的最大值.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由圆![]() 的极坐标方程为
的极坐标方程为![]() ,按照两角和的余弦进行展开,把
,按照两角和的余弦进行展开,把![]() 代入即可得出;(2)把直线的参数方程化为普通方程,利用点到直线的距离公式可得圆心到直线的距离
代入即可得出;(2)把直线的参数方程化为普通方程,利用点到直线的距离公式可得圆心到直线的距离![]() ,再利用弦长公式可得
,再利用弦长公式可得![]() ,利用三角形的面积计算公式即可得出.
,利用三角形的面积计算公式即可得出.
试题解析:(1)圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
即![]() ,
,
所以圆心坐标为![]() ,圆心极坐标为
,圆心极坐标为![]() ,
,
(2)直线![]() 的普通方程为
的普通方程为![]() ,
,
圆心到直线![]() 的距离
的距离 ,
,
所以![]() ,
,
点![]() 到直线
到直线![]() 距离的最大值为
距离的最大值为![]() ,
,
故最大面积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于实数
 和两定点
和两定点 ,在某图形上恰有
,在某图形上恰有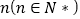 个不同的点
个不同的点 ,使得
,使得 ,称该图形满足“
,称该图形满足“ 度契合”.若边长为4的正方形
度契合”.若边长为4的正方形 中,
中, ,且该正方形满足“4度契合”,则实数
,且该正方形满足“4度契合”,则实数 的取值范围是__________.
的取值范围是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,圆
中,圆 :
: 与
与 轴的正半轴交于点
轴的正半轴交于点 ,以点
,以点 为圆心的圆
为圆心的圆 :
: 与圆
与圆 交于
交于 ,
, 两点.
两点.(1)当
 时,求
时,求 的长;
的长;(2)当
 变化时,求
变化时,求 的最小值;
的最小值;(3)过点
 的直线
的直线 与圆A切于点
与圆A切于点 ,与圆
,与圆 分别交于点
分别交于点 ,
, ,若点
,若点 是
是 的中点,试求直线
的中点,试求直线 的方程.
的方程. 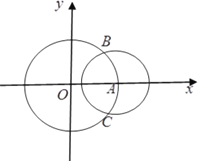
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有
 名学生参加学校组织的“数学竞赛集训队”选拔考试,现从中等可能抽出
名学生参加学校组织的“数学竞赛集训队”选拔考试,现从中等可能抽出 名学生的成绩作为样本,制成如图频率分布表:
名学生的成绩作为样本,制成如图频率分布表:分组
频数
频率

0.025

0.050

0.200
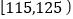
12
0.300

0.275

4

0.00
合计

1
(1)求
 的值,并根据题中信息估计总体平均数是多少?
的值,并根据题中信息估计总体平均数是多少?(2)若成绩不低于
 分的同学能参加“数学竞赛集训队”,试估计该校大约多少名学生能参加“数学竞赛集训队”?
分的同学能参加“数学竞赛集训队”,试估计该校大约多少名学生能参加“数学竞赛集训队”? -
科目: 来源: 题型:
查看答案和解析>>【题目】设双曲线C的焦点在
 轴上,离心率为
轴上,离心率为 ,其一个顶点的坐标是(0,1).
,其一个顶点的坐标是(0,1).(Ⅰ)求双曲线C的标准方程;
(Ⅱ)若直线
 与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线
与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线 的方程
的方程 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆
 过点
过点 ,且与圆
,且与圆 相内切.
相内切.(I)求动圆
 的圆心的轨迹方程;
的圆心的轨迹方程;(II)设直线
 (其中
(其中 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点 ,D,与双曲线
,D,与双曲线 交于不同两点
交于不同两点 ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为实常数) .
为实常数) .(I)当
 时,求函数
时,求函数 在
在 上的最大值及相应的
上的最大值及相应的 值;
值;(II)当
 时,讨论方程
时,讨论方程 根的个数.
根的个数.(III)若
 ,且对任意的
,且对任意的 ,都有
,都有 ,求
,求实数a的取值范围.
相关试题

