【题目】在单调递增数列![]() 中,
中,![]() ,
,![]() ,且
,且![]() 成等差数列,
成等差数列,![]() 成等比数列,
成等比数列,![]() 。
。
(Ⅰ)(ⅰ)求证:数列![]() 为等差数列;
为等差数列;
(ⅱ)求数列![]() 的通项公式。
的通项公式。
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() ,
,![]() 。
。
参考答案:
【答案】(1)紧扣等差数列定义证明,(2)当![]() 为偶数时
为偶数时![]()
![]() ,当
,当![]() 为奇数时
为奇数时![]()
![]() 。(3)证明见解析。
。(3)证明见解析。
【解析】
试题分析:要证明数列![]() 为等差数列,只需证明
为等差数列,只需证明![]()
![]() 成立,由于数列首项为正,
成立,由于数列首项为正,
数列为单调递增,说以![]() ,由
,由![]() 成等差数列,得
成等差数列,得![]() ……(1),由因为
……(1),由因为![]()
![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,![]() 于是
于是![]() 代入(1)式整理得:
代入(1)式整理得:![]()
![]() 得证;先求
得证;先求![]() ,
,![]() 备用,由于数列
备用,由于数列![]() 为等差数列,可借助等差数列通项公式求出
为等差数列,可借助等差数列通项公式求出![]() ,再由
,再由![]() 求出
求出![]() ,最后分
,最后分![]() 为奇数和偶数两种情况表达
为奇数和偶数两种情况表达![]() ,由于数列的通项公式分
,由于数列的通项公式分![]() 为奇数和偶数两种情况表达的,所以需要合在一起,合成公式是
为奇数和偶数两种情况表达的,所以需要合在一起,合成公式是![]()
![]() ,合成后对
,合成后对![]() 进行放缩,这里技巧很重要,
进行放缩,这里技巧很重要,![]()
![]()
![]() ,再求
,再求![]() ,最后利用裂项相消法求和达到证明不等式的目的;
,最后利用裂项相消法求和达到证明不等式的目的;
试题解析:(ⅰ)因为数列![]() 为单调递增数列,
为单调递增数列,![]() ,所以
,所以![]() (
(![]() )。由题意
)。由题意![]() 成等差数列,
成等差数列,![]() 成等比数列,
成等比数列,![]() .得
.得![]()
![]() ,
,![]() ,于是
,于是![]()
![]() ,化简得
,化简得![]()
![]() ,所以数列
,所以数列![]() 为等差数列。
为等差数列。
(ⅱ)又![]() ,
,![]() ,所以数列
,所以数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,所以
,所以![]() ,从而
,从而![]() 。结合
。结合![]() 可得
可得![]() 。因此,当
。因此,当![]() 为偶数时
为偶数时![]()
![]() ,当
,当![]() 为奇数时
为奇数时![]()
![]() 。
。
(2)所以数列![]() 的通项公式为:
的通项公式为:
![]()
![]() 。因
。因![]()
![]()
![]() ,所以
,所以![]() ;则有
;则有![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,所以
,所以![]() ,
,![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在点(1,f(1))处的切线为y=1.
在点(1,f(1))处的切线为y=1.(1)求a,b的值;
(2)问是否存在实数m,使得当x∈(0,1]时,
 的最小值为0?若存在求出m的取值范围;若不存在,请说明理由.
的最小值为0?若存在求出m的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察以下5个等式:
-1=-1
-1+3=2
-1+3-5=-3
-1+3-5+7=4
-1+3-5+7-9=-5
……
根据以上式子规律:
(1)写出第6个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明上述所猜想的第n个等式成立.(n∈N*)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在四棱锥
 中,
中, 面
面 ,
, ,
, ,
, ,
, ,
,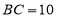 ,
, ,
, 为
为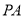 的中点。
的中点。(1)求证:
 面
面 ;
;(2)线段
 上是否存在一点
上是否存在一点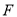 ,满足
,满足 ?若存在,试求出二面角
?若存在,试求出二面角 的余弦值;若不存在,说明理由。
的余弦值;若不存在,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知从
 地到
地到 地共有两条路径
地共有两条路径 和
和 ,据统计,经过两条路径所用的时间互不影响,且经过
,据统计,经过两条路径所用的时间互不影响,且经过 和
和 所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。
所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。
现甲、乙两人分别有40分钟和50分钟时间用于从
 地到
地到 地。
地。(1)为了尽最大可能在各自允许的时间内赶到
 地,甲和乙应如何选择各自的路径?
地,甲和乙应如何选择各自的路径?(2)用
 表示甲、乙两人中在允许的时间内能赶到
表示甲、乙两人中在允许的时间内能赶到 地的人数,针对(1)的选择方案,求
地的人数,针对(1)的选择方案,求 的分布列和数学期望。
的分布列和数学期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
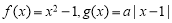 。
。(Ⅰ)若当
 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(Ⅱ)求函数
 在区间
在区间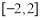 上的最大值。
上的最大值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<
 )为多大时,水渠中水的流失量最小?
)为多大时,水渠中水的流失量最小?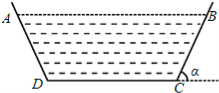
相关试题

