【题目】观察以下5个等式:
-1=-1
-1+3=2
-1+3-5=-3
-1+3-5+7=4
-1+3-5+7-9=-5
……
根据以上式子规律:
(1)写出第6个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明上述所猜想的第n个等式成立.(n∈N*)
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)先写出第六个等式,再用归纳推理猜想出结论;(2)借助题设条件运用数学归纳法求解.
试题解析:
(1)第6个等式为-1+3-5+7-9+11=6
第n个等式为 -1+3-5+7-9+……+(-1)n(2n-1)=(-1)nn
(2)下面用数学归纳法给予证明:
-1+3-5+7-9+……+![]() (2n-1)=
(2n-1)=![]() n
n
(1)当![]() 时,由已知得原式成立;
时,由已知得原式成立;
(2)假设当![]() 时,原式成立,
时,原式成立,
即-1+3-5+7-9+……+(-1)k (2k-1)=(-1)kk
那么,当![]() 时,
时,
-1+3-5+7-9+……+![]() (2k-1)+
(2k-1)+![]() (2k+1)=
(2k+1)=![]() k+
k+![]() (2k+1)
(2k+1)
=![]() (-k+2k+1)
(-k+2k+1)
=(-1)k+1 (k+1)
故当![]() 时,原式也成立.
时,原式也成立.
由(1)(2)可知:-1+3-5+7-9+……+![]() (2n-1)=
(2n-1)=![]() n对n∈N*都成立。
n对n∈N*都成立。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知小矩形花坛ABCD中,AB=3m,AD=2m,现要将小矩形花坛建成大矩形花坛AMPN,使点B在AM上,点D在AN上,且对角线MN过点C.

(1)要使矩形AMPN的面积大于32m2,AN的长应在什么范围内?
(2)M,N是否存在这样的位置,使矩形AMPN的面积最小?若存在,求出这个最小面积及相应的AM。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家拟在2016年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)
 万件与年促销费用
万件与年促销费用 万元(
万元( )满足
)满足 为常数),如果不搞促销活动,则该产品的年销售只能是
为常数),如果不搞促销活动,则该产品的年销售只能是 万件.已知2016 年生产该产品的固定投入为
万件.已知2016 年生产该产品的固定投入为 万元.每生产
万元.每生产 万件该产品需要再投入
万件该产品需要再投入 万元,厂家将每件产品的销售价格定为每件产品年平均成本的
万元,厂家将每件产品的销售价格定为每件产品年平均成本的 倍(产品成本包括固定投入和再投入两部分资金)
倍(产品成本包括固定投入和再投入两部分资金)(1)将2016 年该产品的利润
 万元表示为年促销费用
万元表示为年促销费用 万元的函数;
万元的函数;(2)该厂家2016 年的促销费用投入多少万元时,厂家的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在点(1,f(1))处的切线为y=1.
在点(1,f(1))处的切线为y=1.(1)求a,b的值;
(2)问是否存在实数m,使得当x∈(0,1]时,
 的最小值为0?若存在求出m的取值范围;若不存在,请说明理由.
的最小值为0?若存在求出m的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在四棱锥
 中,
中, 面
面 ,
, ,
, ,
, ,
, ,
,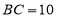 ,
, ,
, 为
为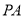 的中点。
的中点。(1)求证:
 面
面 ;
;(2)线段
 上是否存在一点
上是否存在一点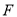 ,满足
,满足 ?若存在,试求出二面角
?若存在,试求出二面角 的余弦值;若不存在,说明理由。
的余弦值;若不存在,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在单调递增数列
 中,
中, ,
, ,且
,且 成等差数列,
成等差数列, 成等比数列,
成等比数列, 。
。(Ⅰ)(ⅰ)求证:数列
 为等差数列;
为等差数列;(ⅱ)求数列
 的通项公式。
的通项公式。(Ⅱ)设数列
 的前
的前 项和为
项和为 ,证明:
,证明: ,
, 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知从
 地到
地到 地共有两条路径
地共有两条路径 和
和 ,据统计,经过两条路径所用的时间互不影响,且经过
,据统计,经过两条路径所用的时间互不影响,且经过 和
和 所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。
所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。
现甲、乙两人分别有40分钟和50分钟时间用于从
 地到
地到 地。
地。(1)为了尽最大可能在各自允许的时间内赶到
 地,甲和乙应如何选择各自的路径?
地,甲和乙应如何选择各自的路径?(2)用
 表示甲、乙两人中在允许的时间内能赶到
表示甲、乙两人中在允许的时间内能赶到 地的人数,针对(1)的选择方案,求
地的人数,针对(1)的选择方案,求 的分布列和数学期望。
的分布列和数学期望。
相关试题

