【题目】已知函数![]() 。
。
(Ⅰ)若当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最大值。
上的最大值。
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时,
时,![]() 在
在![]() 上的最大值为
上的最大值为![]() ;当
;当![]() 时,
时,![]() 在
在![]() 上的最大值为
上的最大值为![]() ;当
;当![]() 时,
时,![]() 在
在![]() 上的最大值为0。
上的最大值为0。
【解析】
试题分析:(Ⅰ)按照x与1进行讨论,分离常数得![]() ,令
,令![]() ,去掉绝对值符号化简解析式,由一次函数的性质分别求出
,去掉绝对值符号化简解析式,由一次函数的性质分别求出![]() 的范围,由恒成立问题求出
的范围,由恒成立问题求出![]() 的范围,最后取并集;(Ⅱ)由题意求出
的范围,最后取并集;(Ⅱ)由题意求出![]() ,按照x与1、-1的关系去掉绝对值符号化简解析式,由区间和对称轴对
,按照x与1、-1的关系去掉绝对值符号化简解析式,由区间和对称轴对![]() 进行分类讨论,分别由二次函数的性质判断出
进行分类讨论,分别由二次函数的性质判断出![]() h(x)在区间上的单调性,并求出对应的最大值。
h(x)在区间上的单调性,并求出对应的最大值。
试题解析:解:(1)不等式![]() 对
对![]() 恒成立,即
恒成立,即![]() ()对
()对![]() 恒成立,①当
恒成立,①当![]() 时,()显然成立,此时
时,()显然成立,此时![]() ;②当
;②当![]() 时,()可变形为
时,()可变形为![]() ,令
,令![]()
因为当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,故此时
,故此时![]() 。综合①②,得所求实数
。综合①②,得所求实数![]() 的取值范围是
的取值范围是![]() 。
。
(2)因为![]() =
= ①当
①当![]() 时,结合图形可知
时,结合图形可知![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,且
上递增,且![]() ,经比较,此时
,经比较,此时![]() 在
在![]() 上的最大值为
上的最大值为![]() 。
。
②当![]() 时,结合图形可知
时,结合图形可知![]() 在
在![]() ,
,![]() 上递减,在
上递减,在![]() ,
,![]() 上递增,且
上递增,且![]() ,
,![]() ,经比较,知此时
,经比较,知此时![]() 在
在![]() 上的最大值为
上的最大值为![]() 。
。
③当![]() 时,结合图形可知
时,结合图形可知![]() 在
在![]() ,
,![]() 上递减,在
上递减,在![]() ,
,![]() 上递增,且
上递增,且![]() ,
,![]() ,经比较,知此时
,经比较,知此时![]() 在
在![]() 上的最大值为
上的最大值为![]() 。
。
④当![]() 时,结合图形可知
时,结合图形可知![]() 在
在![]() ,
,![]() 上递减,在
上递减,在![]() ,
,![]() 上递增,且
上递增,且![]() ,
, ![]() ,经比较,知此时
,经比较,知此时![]() 在
在![]() 上的最大值为
上的最大值为![]() 。
。
当![]() 时,结合图形可知
时,结合图形可知![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,故此时
上递增,故此时![]() 在
在![]() 上的最大值为
上的最大值为![]() 。综上所述,当
。综上所述,当![]() 时,
时,![]() 在
在![]() 上的最大值为
上的最大值为![]() ;当
;当![]() 时,
时,![]() 在
在![]() 上的最大值为
上的最大值为![]() ;当
;当![]() 时,
时,![]() 在
在![]() 上的最大值为0。
上的最大值为0。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在四棱锥
 中,
中, 面
面 ,
, ,
, ,
, ,
, ,
,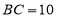 ,
, ,
, 为
为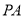 的中点。
的中点。(1)求证:
 面
面 ;
;(2)线段
 上是否存在一点
上是否存在一点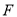 ,满足
,满足 ?若存在,试求出二面角
?若存在,试求出二面角 的余弦值;若不存在,说明理由。
的余弦值;若不存在,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在单调递增数列
 中,
中, ,
, ,且
,且 成等差数列,
成等差数列, 成等比数列,
成等比数列, 。
。(Ⅰ)(ⅰ)求证:数列
 为等差数列;
为等差数列;(ⅱ)求数列
 的通项公式。
的通项公式。(Ⅱ)设数列
 的前
的前 项和为
项和为 ,证明:
,证明: ,
, 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知从
 地到
地到 地共有两条路径
地共有两条路径 和
和 ,据统计,经过两条路径所用的时间互不影响,且经过
,据统计,经过两条路径所用的时间互不影响,且经过 和
和 所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。
所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。
现甲、乙两人分别有40分钟和50分钟时间用于从
 地到
地到 地。
地。(1)为了尽最大可能在各自允许的时间内赶到
 地,甲和乙应如何选择各自的路径?
地,甲和乙应如何选择各自的路径?(2)用
 表示甲、乙两人中在允许的时间内能赶到
表示甲、乙两人中在允许的时间内能赶到 地的人数,针对(1)的选择方案,求
地的人数,针对(1)的选择方案,求 的分布列和数学期望。
的分布列和数学期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<
 )为多大时,水渠中水的流失量最小?
)为多大时,水渠中水的流失量最小?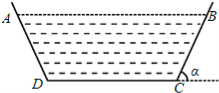
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 。
。(1)求函数
 的单调区间;
的单调区间;(2)当
 时,设函数
时,设函数 ,若对于
,若对于 使
使 成立,求实数
成立,求实数 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】
已知函数
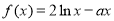 ,
,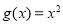 。
。(1)若函数
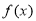 在
在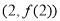 处的切线与函数
处的切线与函数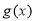 在
在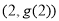 处的切线互相平行,求实数
处的切线互相平行,求实数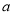 的值;
的值;(2)设函数
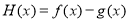 。
。(ⅰ)当实数
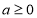 时,试判断函数
时,试判断函数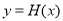 在
在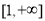 上的单调性;
上的单调性;(ⅱ)如果
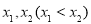 是
是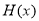 的两个零点,
的两个零点,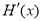 为函数
为函数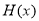 的导函数,证明:
的导函数,证明: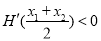 。
。
相关试题

