【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数![]() 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 的单调递减区间.
的单调递减区间.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由两相邻对称轴间的距离为![]() 可得半个周期为
可得半个周期为![]() .进而求出
.进而求出![]() ,由偶函数可得
,由偶函数可得![]() ,由三角函数恒等变形可得
,由三角函数恒等变形可得![]() .代入自变量
.代入自变量![]() 即得
即得![]() 的值;(2)先根据图像变换得到
的值;(2)先根据图像变换得到![]() 的解析式
的解析式![]() .再根据余弦函数性质求
.再根据余弦函数性质求![]() 的单调递减区间.
的单调递减区间.
试题解析: 解:(1)∵![]() 为偶函数,
为偶函数,
∴对![]() 恒成立,∴
恒成立,∴![]() .
.
即:![]()
又∵![]() ,故
,故![]() .
.
∴![]()
由题意得![]() ,所以
,所以![]()
故![]() ,∴
,∴![]()
(2)将![]() 的图象向右平移
的图象向右平移![]() 个单位后,得到
个单位后,得到![]() 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到![]() 的图象.
的图象.
∴![]() .
.
当![]() ,
,
即![]() 时,
时,![]() 单调递减,
单调递减,
因此![]() 的单调递减区间为
的单调递减区间为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点,焦点在
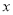 轴上的椭圆,离心率为
轴上的椭圆,离心率为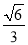 且过点
且过点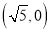 ,过定点
,过定点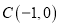 的动直线与该椭圆相交于
的动直线与该椭圆相交于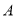 、
、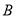 两点.
两点.(1)若线段
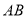 中点的横坐标是
中点的横坐标是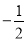 ,求直线
,求直线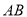 的方程;
的方程;(2)在
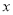 轴上是否存在点
轴上是否存在点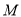 ,使
,使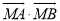 为常数?若存在,求出点
为常数?若存在,求出点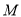 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,圆
,圆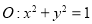 .
.(1)若抛物线
 的焦点
的焦点 在圆上,且
在圆上,且 为
为  和圆
和圆  的一个交点,求
的一个交点,求 ;
;(2)若直线
 与抛物线
与抛物线 和圆
和圆 分别相切于点
分别相切于点 ,求
,求 的最小值及相应
的最小值及相应 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为
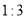 ,且成绩分布在
,且成绩分布在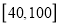 ,分数在
,分数在 以上(含
以上(含 )的同学获奖. 按文理科用分层抽样的方法抽取
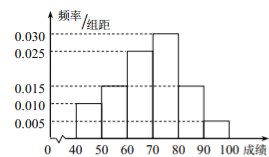
)的同学获奖. 按文理科用分层抽样的方法抽取 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).(1)填写下面的
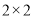 列联表,能否有超过
列联表,能否有超过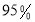 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取
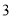 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为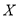 ,求
,求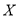 的分布列及数学期望.
的分布列及数学期望.文科生
理科生
合计
获奖
不获奖
合计

附表及公式:
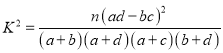 ,其中
,其中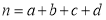
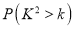

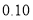

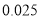
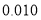
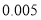
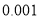
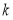

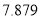
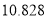
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年利润
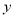 (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费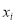 和年利润
和年利润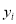 (
(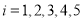 )进行了统计,列出了下表:
)进行了统计,列出了下表: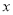 (单位:千元)
(单位:千元)2
4
7
17
30
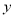 (单位:万元)
(单位:万元)1
2
3
4
5
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合
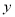 与
与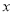 的关系,请你帮助建立
的关系,请你帮助建立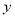 关于
关于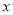 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)(2)小李决定选择对数回归模型拟合
 与
与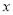 的关系,得到了回归方程:
的关系,得到了回归方程: 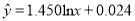 ,并提供了相关指数
,并提供了相关指数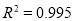 .请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据
.请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据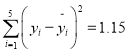 )
)参考公式:相关指数
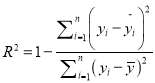
回归方程
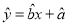 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: 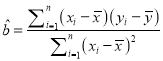 ,
, 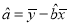 .参考数据:
.参考数据: 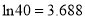 ,
, 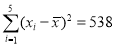 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(1)求函数
 在
在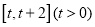 的最小值;
的最小值; (2)若函数
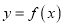 与
与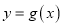 的图象恰有一个公共点,求实数
的图象恰有一个公共点,求实数 的值;
的值;(3)若函数
 有两个不同的极值点
有两个不同的极值点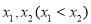 ,且
,且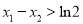 ,求实数
,求实数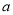 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,底面
中,底面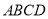 是边长为
是边长为 的菱形,
的菱形, ,
, .
.
(1)证明:
 平面
平面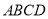 ;
;(2)若
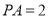 ,求二面角
,求二面角 的余弦值.
的余弦值.
相关试题

