【题目】(本小题满分12分)已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线![]() 的焦点重合,过点
的焦点重合,过点![]() 且不垂直于
且不垂直于![]() 轴的直线
轴的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设椭圆的方程,若焦点明确,设椭圆的标准方程,结合条件用待定系数法求出![]() 的值,若不明确,需分焦点在
的值,若不明确,需分焦点在![]() 轴和
轴和![]() 轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式![]() :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:解:(1)由题意知![]() ,
,
![]() .又双曲线的焦点坐标为
.又双曲线的焦点坐标为![]() ,
, ![]() ,
,
![]() 椭圆的方程为
椭圆的方程为![]() .
.
(2)若直线![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]() ,
,
当直线![]() 的倾斜角不为
的倾斜角不为![]() 时,直线
时,直线![]() 可设为
可设为![]() ,
,
![]() ,由
,由
![]()
设![]() ,
, ![]() ,
,
![]()
![]() ,
, ![]() ,综上所述:范围为
,综上所述:范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,侧棱垂直于底面,
中,侧棱垂直于底面,  ,
,  ,
,  是棱
是棱 的中点.
的中点.
(Ⅰ)证明:平面
 ⊥平面
⊥平面 ;
;(Ⅱ)求异面直线
 与
与 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一批材料可以建成100m长的围墙,现用这些材料在一边靠墙的地方围成一块封闭的矩形场地,中间隔成3个面积相等的小矩形(如图),则围成的矩形场地的最大总面积为(围墙厚度忽略不计)m2 .
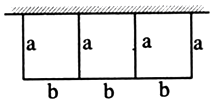
-
科目: 来源: 题型:
查看答案和解析>>【题目】有三支股票
 ,
, 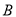 ,
, 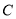 ,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有
,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有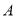 股票的人中,持有
股票的人中,持有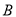 股票的人数是持有
股票的人数是持有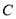 股票的人数的2倍.在持有
股票的人数的2倍.在持有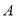 股票的人中,只持有
股票的人中,只持有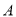 股票的人数比除了持有
股票的人数比除了持有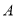 股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有
股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有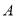 股票.则只持有
股票.则只持有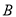 股票的股民人数是( )
股票的股民人数是( )A.
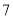 B.
B. 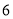 C.
C. 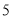 D.
D. 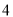
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
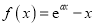 .
.(Ⅰ)若曲线
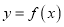 在
在 处的切线
处的切线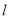 与直线
与直线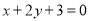 垂直,求
垂直,求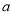 的值;
的值;(Ⅱ)当
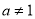 时,求证:存在实数
时,求证:存在实数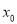 使
使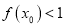 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (x∈R),e是自然对数的底.
(x∈R),e是自然对数的底.
(1)计算f(ln2)的值;
(2)证明函数f(x)是奇函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱锥
 ,侧棱
,侧棱 ,底面三角形
,底面三角形 为正三角形,边长为
为正三角形,边长为 ,顶点
,顶点 在平面
在平面 上的射影为
上的射影为 ,有
,有 ,且
,且 .
.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值;
的余弦值;(Ⅲ)线段
 上是否存在点
上是否存在点 使得
使得 ⊥平面
⊥平面 ,如果存在,求
,如果存在,求 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
相关试题

