【题目】一批材料可以建成100m长的围墙,现用这些材料在一边靠墙的地方围成一块封闭的矩形场地,中间隔成3个面积相等的小矩形(如图),则围成的矩形场地的最大总面积为(围墙厚度忽略不计)m2 . 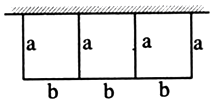
参考答案:
【答案】625
【解析】解:设每个小矩形的高为am,则长为b= ![]() (100﹣4a)m,记面积为Sm2
(100﹣4a)m,记面积为Sm2
则S=3ab=a(100﹣4a)=﹣4a2+100a=﹣4(a﹣ ![]() )2+625(0<a<25)
)2+625(0<a<25)
∴当a=12.5时,Smax=625(m2)
∴所围矩形面积的最大值为625m2
所以答案是625.
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识,掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
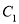 :
: 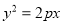 与椭圆
与椭圆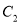 :
: 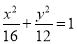 在第一象限的交点为
在第一象限的交点为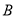 ,
, 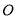 为坐标原点,
为坐标原点, 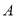 为椭圆的右顶点,
为椭圆的右顶点, 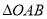 的面积为
的面积为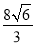 .
.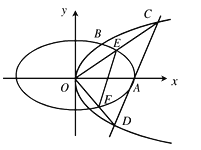
(Ⅰ)求抛物线
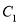 的方程;
的方程;(Ⅱ)过
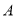 点作直线
点作直线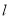 交
交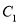 于
于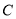 、
、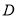 两点,射线
两点,射线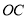 、
、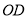 分别交
分别交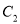 于
于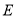 、
、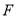 两点,记
两点,记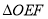 和
和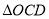 的面积分别为
的面积分别为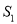 和
和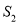 ,问是否存在直线
,问是否存在直线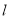 ,使得
,使得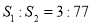 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
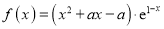 ,其中
,其中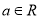 .
.(Ⅰ)求函数
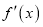 的零点个数;
的零点个数;(Ⅱ)证明:
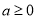 是函数
是函数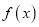 存在最小值的充分而不必要条件.
存在最小值的充分而不必要条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,侧棱垂直于底面,
中,侧棱垂直于底面,  ,
,  ,
,  是棱
是棱 的中点.
的中点.
(Ⅰ)证明:平面
 ⊥平面
⊥平面 ;
;(Ⅱ)求异面直线
 与
与 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有三支股票
 ,
, 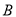 ,
, 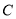 ,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有
,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有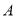 股票的人中,持有
股票的人中,持有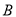 股票的人数是持有
股票的人数是持有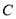 股票的人数的2倍.在持有
股票的人数的2倍.在持有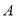 股票的人中,只持有
股票的人中,只持有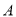 股票的人数比除了持有
股票的人数比除了持有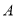 股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有
股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有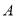 股票.则只持有
股票.则只持有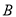 股票的股民人数是( )
股票的股民人数是( )A.
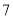 B.
B. 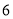 C.
C. 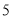 D.
D. 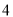
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)已知椭圆
 的离心率为
的离心率为 ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线 的焦点重合,过点
的焦点重合,过点 且不垂直于
且不垂直于 轴的直线
轴的直线 与椭圆
与椭圆 相交于
相交于 两点.
两点.(1)求椭圆
 的方程;
的方程;(2)求
 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
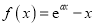 .
.(Ⅰ)若曲线
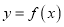 在
在 处的切线
处的切线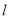 与直线
与直线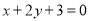 垂直,求
垂直,求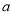 的值;
的值;(Ⅱ)当
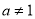 时,求证:存在实数
时,求证:存在实数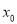 使
使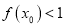 .
.
相关试题

