【题目】已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a=3,b=-9时,若函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]() 的取值范围是
的取值范围是![]()
【解析】试题分析:(1)求a,b的值,根据曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,列方程组,即可求出
处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,列方程组,即可求出![]() 的值;(2)求k的取值范围.,先求出
的值;(2)求k的取值范围.,先求出![]() 的解析式,由已知
的解析式,由已知![]() 时,设
时,设![]() ,求导函数,确定函数的极值点,进而可得
,求导函数,确定函数的极值点,进而可得![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ;
; ![]() 时,函数
时,函数![]() 在在区间
在在区间![]() 上的最大值小于
上的最大值小于![]() ,由此可得结论.
,由此可得结论.
试题解析:(1)![]() ,因为曲线
,因为曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,所以
处具有公共切线,所以![]() ,所以
,所以![]() ;
;
(2)当![]() 时,
时,![]() ,
, ![]() ,
, ![]() ,令
,令![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 与
与![]() 上单调递增,在
上单调递增,在![]() 上单调递减,其中
上单调递减,其中![]() 为极大值,所以如果在区间
为极大值,所以如果在区间![]() 最大值为
最大值为![]() ,即区间包含极大值点
,即区间包含极大值点![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在几何体
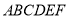 中,平面
中,平面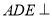 平面
平面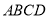 ,四边形
,四边形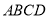 为菱形,且
为菱形,且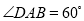 ,
, 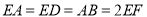 ,
, 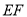 ∥
∥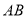 ,
, 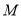 为
为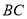 中点.
中点.(Ⅰ)求证:
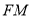 ∥平面
∥平面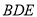 ;
;(Ⅱ)求直线
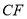 与平面
与平面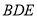 所成角的正弦值;
所成角的正弦值; (Ⅲ)在棱
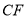 上是否存在点
上是否存在点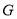 ,使
,使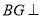
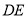 ? 若存在,求
? 若存在,求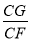 的值;若不存在,说明理由.
的值;若不存在,说明理由.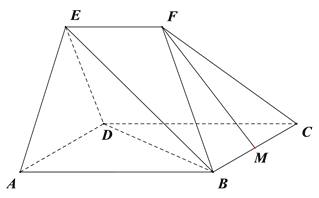
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=-
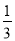 x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,已知四边形
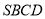 是由直角△
是由直角△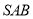 和直角梯形
和直角梯形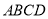 拼接而成的,其中
拼接而成的,其中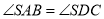
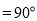 .且点
.且点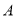 为线段
为线段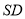 的中点,
的中点, 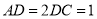 ,
, 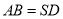 现将△
现将△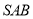 沿
沿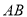 进行翻折,使得二面角
进行翻折,使得二面角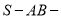
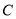 的大小为
的大小为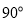 ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接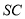 ,点
,点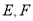 分别在线段
分别在线段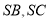 上.
上.

(1)证明:
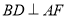 ;
;(2)若三棱锥
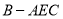 的体积为四棱锥
的体积为四棱锥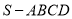 体积的
体积的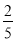 ,求点
,求点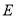 到平面
到平面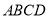 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】某颜料公司生产
 两种产品,其中生产每吨
两种产品,其中生产每吨 产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨
产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨 产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果
产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果 产品的利润为300元/吨,
产品的利润为300元/吨,  产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )A. 14000元 B. 16000元 C. 18000元 D. 20000元
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
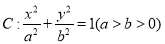 的左、右焦点分别为
的左、右焦点分别为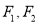 ,点
,点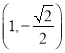 是椭圆
是椭圆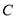 上的点,离心率为
上的点,离心率为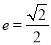 .
.(1)求椭圆
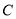 的方程;
的方程;(2)点
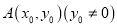 在椭圆上
在椭圆上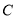 上,若点
上,若点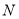 与点
与点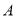 关于原点的对称,连接
关于原点的对称,连接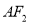 ,并延长与椭圆
,并延长与椭圆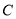 的另一个交点为
的另一个交点为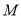 ,连接
,连接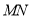 ,求
,求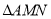 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3 700x+45x2-10x3(单位:万元),成本函数为C(x)=460x-5 000(单位:万元).
(1)求利润函数P(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
相关试题

