【题目】某公司新上一条生产线,为保证新的生产线正常工作,需对该生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数![]() ,标准差
,标准差![]() ,绘制如图所示的频率分布直方图,以频率值作为概率估值.
,绘制如图所示的频率分布直方图,以频率值作为概率估值.
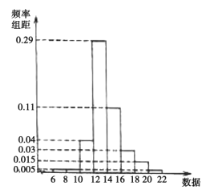
(1)从该生产线加工的产品中任意抽取一件,记其数据为X,依据以下不等式评判(P表示对应事件的概率)
①![]()
②![]()
③![]()
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线,试判断该生产线是否需要检修;
(2)将数据不在![]() 内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为Y,求Y的分布列与数学期望
内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为Y,求Y的分布列与数学期望![]() .
.
参考答案:
【答案】(1)该生产线需检修;(2)分布列详见解析,数学期望为![]() .
.
【解析】
(1)由题意得到![]() ,根据频率分布直方图,求得相应的概率,进行比较,即可得到结论;
,根据频率分布直方图,求得相应的概率,进行比较,即可得到结论;
(2)由(1)得到所以任取一件是次品的概率为![]() ,再得到随机变量Y的可能值,求得相应的概率,得到随机变量的分布列,利用公式求得期望.
,再得到随机变量Y的可能值,求得相应的概率,得到随机变量的分布列,利用公式求得期望.
(1)由题意知,用统计方法得到样本的平均数![]() ,标准差
,标准差![]() ,
,
由频率分布直方图得:
![]() ,
,
![]() ,
,
![]() ,
,
所以不满足至少两个不等式,该生产线需检修.
(2)由(1)知:![]() ,
,
所以任取一件是次品的概率为:![]() ,
,
所以任取两件产品得到次品数Y的可能值为:![]() ,
,
则![]() ,
,![]() ,
,![]()
∴Y的分布列为:
Y | 0 | 1 | 2 |
P |
|
|
|
所以![]() .(或
.(或![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合
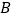 是集合
是集合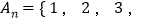 …,
…, 的子集.记
的子集.记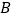 中所有元素的和为
中所有元素的和为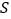 (规定:
(规定: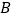 为空集时,
为空集时,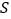 =0).若
=0).若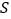 为3的整数倍,则称
为3的整数倍,则称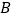 为
为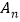 的“和谐子集”.
的“和谐子集”.求:(1)集合
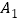 的“和谐子集”的个数;
的“和谐子集”的个数;(2)集合
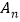 的“和谐子集”的个数.
的“和谐子集”的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级100名学生中进行了抽样调查,发现喜欢甜品的占70%.这100名学生中南方学生共80人.南方学生中有20人不喜欢甜品.
(1)完成下列
 列联表:
列联表:喜欢甜品
不喜欢甜品
合计
南方学生
北方学生
合计
(2)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有6名数学系的学生,其中2名不喜欢甜品;有5名物理系的学生,其中1名不喜欢甜品.现从这两个系的学生中,各随机抽取2人,记抽出的4人中不喜欢甜品的人数为X,求X的分布列和数学期望.
附:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某县教育局为了检查本县甲、乙两所学校的学生对安全知识的学习情况,在这两所学校进行了安全知识测试,随机在这两所学校各抽取20名学生的考试成绩作为样本,成绩大于或等于80分的为优秀,否则为不优秀,统计结果如下图:


甲校 乙校
(1)从乙校成绩优秀的学生中任选两名,求这两名学生的成绩恰有一个落在
 内的概率;
内的概率;(2)由以上数据完成下面列联表,并回答能否在犯错的概率不超过0.1的前提下认为学生的成绩与两所学校的选择有关。
甲校
乙校
总计
优秀
不优秀
总计

参考数据
P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
span>3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线
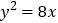 的焦点为
的焦点为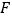 ,其准线与
,其准线与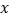 轴的交点为
轴的交点为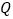 ,过点
,过点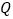 作斜率为
作斜率为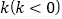 的直线交抛物线于
的直线交抛物线于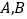 两点,若
两点,若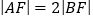 ,则
,则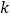 的值为( )
的值为( )A.
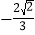 B.
B. 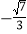 C.
C. 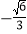 D.
D. 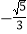
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥中
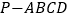 ,四边形
,四边形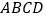 为菱形,
为菱形,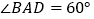 ,
,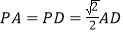 ,平面
,平面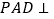 平面
平面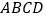 .
.
(1)求证:
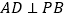 ;
;(2)求二面角
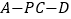 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 为不同的两点,直线
为不同的两点,直线 ,下列命题正确的有( ).
,下列命题正确的有( ).①不论
 为何值,点
为何值,点 都不在直线
都不在直线 上;
上;②若
 ,则过点
,则过点 的直线与直线
的直线与直线 平行;
平行;③若
 ,则直线
,则直线 经过
经过 的中点;
的中点;④若
 ,则点
,则点 在直线
在直线 的同侧且直线
的同侧且直线 与线段
与线段 的延长线相交.
的延长线相交.A.1个B.2个C.3个D.4个
相关试题

