【题目】(本小题满分13分)已知椭圆C的中心在坐标原点,离心率![]() ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线![]() 的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点
的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点![]() 的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
参考答案:
【答案】解:(Ⅰ)设椭圆的方程为![]() ,离心率
,离心率![]() ,
,![]() ,抛物线
,抛物线![]() 的焦点为
的焦点为![]() ,所以
,所以![]() ,椭圆C的方程是x2+
,椭圆C的方程是x2+![]() =1. …………(4分)
=1. …………(4分)
(Ⅱ)若直线l与x轴重合,则以AB为直径的圆是x2+y2=1,若直线l垂直于x轴,则以AB为直径的圆是(x+![]() )2+y2=
)2+y2=![]() .
.
由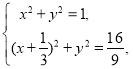 解得
解得![]() 即两圆相切于点(1,0).
即两圆相切于点(1,0).
因此所求的点T如果存在,只能是(1,0).…………(6分)
事实上,点T(1,0)就是所求的点.证明如下:
当直线l垂直于x轴时,以AB为直径的圆过点T(1,0).
若直线l不垂直于x轴,可设直线l:y=k(x+![]() ).由
).由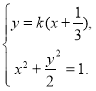 即(k2+2)x2+
即(k2+2)x2+![]() k2x+
k2x+![]() k2-2=0.
k2-2=0.
记点A(x1,y1),B(x2,y2),则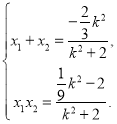 …………(9分)
…………(9分)
又因为![]() =(x1-1, y1),
=(x1-1, y1), ![]() =(x2-1, y2),
=(x2-1, y2),
![]() ·
·![]() =(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+
=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+![]() )(x2+
)(x2+![]() )
)
=(k2+1)x1x2+(![]() k2-1)(x1+x2)+
k2-1)(x1+x2)+![]() k2+1 =(k2+1)
k2+1 =(k2+1) 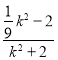 +(
+(![]() k2-1)
k2-1) ![]() +
+ ![]() +1=0,
+1=0,
所以TA⊥TB,即以AB为直径的圆恒过点T(1,0).
所以在坐标平面上存在一个定点T(1,0)满足条件. …………(13分)
【解析】略
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:

组别分组
频数
频率
第1组
[50,60)
8
0 16
第2组
[60,70)
a
▓
第3组
[70,80)
20
0 40
第4组
[80,90)
▓
0 08
第5组
[90,100]
2
b
合计
▓
▓

(1)求出
 的值;
的值;(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 经过点
经过点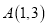 、
、 ,并且直线
,并且直线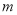 :
:  平分圆
平分圆 .
.(Ⅰ)求圆
 的方程;
的方程;(Ⅱ)若过点
 ,且斜率为
,且斜率为 的直线
的直线 与圆
与圆 有两个不同的交点
有两个不同的交点 .
.(ⅰ)求实数
 的取值范围;
的取值范围;(ⅱ)若
 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我海监船在
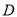 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至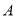 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距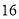 海里的
海里的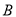 处有一外国船只,且
处有一外国船只,且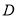 岛位于海监船正东
岛位于海监船正东 海里处。
海里处。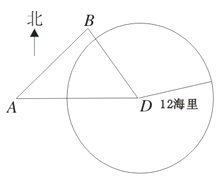
(Ⅰ)求此时该外国船只与
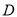 岛的距离;
岛的距离;(Ⅱ)观测中发现,此外国船只正以每小时
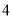 海里的速度沿正南方向航行。为了将该船拦截在离
海里的速度沿正南方向航行。为了将该船拦截在离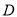 岛
岛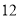 海里处,不让其进入
海里处,不让其进入 岛
岛 海里内的海域,试确定海监船的航向,并求其速度的最小值.
海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
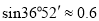 ,
, 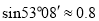 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】三国魏人刘徽,自撰《海岛算经》,专论测高望远。其中有一题:今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高及去表各几何? 译文如下:要测量海岛上一座山峰
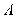 的高度
的高度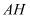 ,立两根高均为
,立两根高均为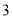 丈的标杆
丈的标杆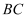 和
和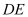 ,前后标杆相距
,前后标杆相距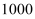 步,使后标杆杆脚
步,使后标杆杆脚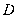 与前标杆杆脚
与前标杆杆脚 与山峰脚
与山峰脚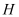 在同一直线上,从前标杆杆脚
在同一直线上,从前标杆杆脚 退行
退行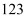 步到
步到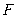 ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,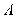 、
、 、
、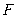 三点共线,从后标杆杆脚
三点共线,从后标杆杆脚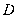 退行
退行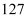 步到
步到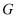 ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,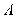 、
、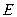 、
、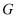 三点也共线,问岛峰的高度
三点也共线,问岛峰的高度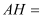 步. (古制:
步. (古制: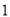 步=
步=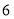 尺,
尺,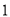 里=
里=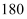 丈=
丈=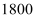 尺=
尺=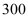 步)
步) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
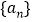 的前
的前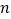 项和为
项和为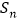 ,且
,且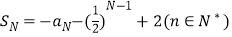 .
.(1)求数列
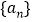 的通项公式,并写出推理过程;
的通项公式,并写出推理过程;(2)令
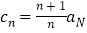 ,
,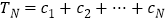 ,试比较
,试比较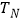 与
与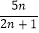 的大小,并给出你的证明.
的大小,并给出你的证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
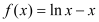 .
.(1)求函数
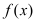 的单调区间;
的单调区间;(2)若方程

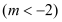 有两个相异实根
有两个相异实根 ,
,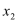 ,且
,且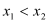 ,证明:
,证明: .
.
相关试题

