【题目】某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
![]()
| 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0 16 |
第2组 | [60,70) | a | ▓ |
第3组 | [70,80) | 20 | 0 40 |
第4组 | [80,90) | ▓ | 0 08 |
第5组 | [90,100] | 2 | b |
合计 | ▓ | ▓ |

(1)求出![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率
参考答案:
【答案】(1)![]() .(2)(ⅰ)
.(2)(ⅰ)![]() .(ⅱ)
.(ⅱ)![]()
【解析】试题分析:(1)首先由第一组或第三组可得样本容量为50 由此可得![]() ,由此得第二组的频率为
,由此得第二组的频率为![]() ,所以
,所以![]() .由
.由![]() 得
得![]() ;(2)(ⅰ)80分以上即在第四组和第五组 第4组共有4人,记为
;(2)(ⅰ)80分以上即在第四组和第五组 第4组共有4人,记为![]() ,第5组 共有2人,记为
,第5组 共有2人,记为![]() .从这6名同学中随机抽取2名同学有
.从这6名同学中随机抽取2名同学有![]() ,
, ![]() 共15种情况.设“随机抽取的2名同学中至少有1名同学来自第5组”
共15种情况.设“随机抽取的2名同学中至少有1名同学来自第5组”
有![]() ,
, ![]() 共9种情况.由此即可得所求概率 (ⅱ)2名同学来自同一组有
共9种情况.由此即可得所求概率 (ⅱ)2名同学来自同一组有![]() 共7种情况.由此可得所求概率
共7种情况.由此可得所求概率
试题解析:(1)由题意可知, ![]() . (4分)
. (4分)
(2)(ⅰ)由题意可知,第4组共有4人,记为![]() ,第5组共有2人,记为
,第5组共有2人,记为![]() .
.
从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有![]() ,
, ![]()
共15种情况. (6分)
设“随机抽取的2名同学中至少有1名同学来自第5组”为事件![]() ,
,
有![]() ,
, ![]() 共9种情况. (9分)
共9种情况. (9分)
所以随机抽取的2名同学中至少有1名同学来自第5组的概率是![]() . (10分)
. (10分)
(ⅱ)设“随机抽取的2名同学来自同一组”为事件![]() ,有
,有![]() 共7种情况.
共7种情况.
所以随机抽取的2名同学来自同一组的概率![]() (12分)
(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数
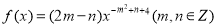 为偶函数,且在区间
为偶函数,且在区间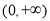 上是单调递增函数。
上是单调递增函数。(Ⅰ)求函数
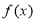 的解析式;
的解析式;(Ⅱ)设
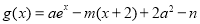 ,若
,若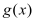 能取遍
能取遍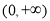 内的所有实数,求实数
内的所有实数,求实数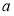 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为选拔参加“全市高中数学竞赛”的选手,某中学举行了一次“数学竞赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为
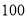 分)作为样本(样本容量为
分)作为样本(样本容量为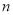 )进行统计.按照
)进行统计.按照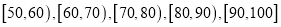 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在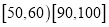 的数据).
的数据).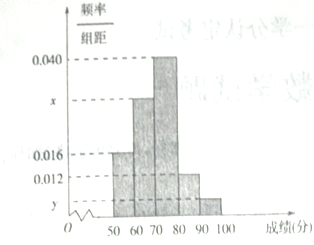
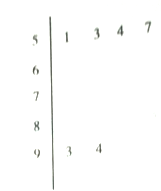
(1)求样本容
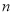 和频率分布直方图中
和频率分布直方图中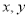 的值并求出抽取学生的平均分;
的值并求出抽取学生的平均分;(2)在选取的样本中,从竞赛成绩在
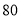 分以上(含
分以上(含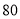 分)的学生中随机抽取
分)的学生中随机抽取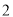 名学生参加“全市中数学竞赛”求所抽取的
名学生参加“全市中数学竞赛”求所抽取的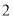 名学生中至少有一人得分在
名学生中至少有一人得分在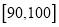 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是块矩形硬纸板,其中AB=2AD,AD=
 ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.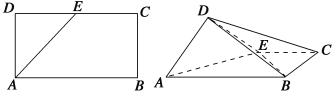
(1)求证:AD⊥平面BDE;
(2)求二面角B-AD-E的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 经过点
经过点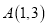 、
、 ,并且直线
,并且直线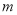 :
:  平分圆
平分圆 .
.(Ⅰ)求圆
 的方程;
的方程;(Ⅱ)若过点
 ,且斜率为
,且斜率为 的直线
的直线 与圆
与圆 有两个不同的交点
有两个不同的交点 .
.(ⅰ)求实数
 的取值范围;
的取值范围;(ⅱ)若
 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我海监船在
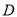 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至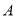 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距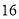 海里的
海里的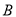 处有一外国船只,且
处有一外国船只,且 岛位于海监船正东
岛位于海监船正东 海里处。
海里处。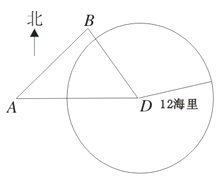
(Ⅰ)求此时该外国船只与
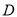 岛的距离;
岛的距离;(Ⅱ)观测中发现,此外国船只正以每小时
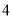 海里的速度沿正南方向航行。为了将该船拦截在离
海里的速度沿正南方向航行。为了将该船拦截在离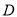 岛
岛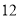 海里处,不让其进入
海里处,不让其进入 岛
岛 海里内的海域,试确定海监船的航向,并求其速度的最小值.
海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
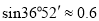 ,
, 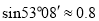 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分13分)已知椭圆C的中心在坐标原点,离心率
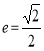 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线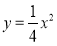 的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点
的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点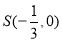 的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
相关试题

