【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若方程![]()
![]() 有两个相异实根
有两个相异实根![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
参考答案:
【答案】(1)增区间![]() ,减区间
,减区间![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)求出导函数![]() ,在函数定义或内,通过解不等式
,在函数定义或内,通过解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;(2)要证明题设不等式,首先要确定
得减区间;(2)要证明题设不等式,首先要确定![]() 的性质.由(1)函数的单调性知
的性质.由(1)函数的单调性知![]() ,同时由
,同时由![]() 得,
得,![]() ,从而
,从而![]() ,从要证明的结论可以看出 ,我们要证明
,从要证明的结论可以看出 ,我们要证明![]() ,由于
,由于![]() 在
在![]() 上是递增的,因此可证
上是递增的,因此可证![]() ,作差
,作差![]() ,
,![]()
![]()
![]()
![]() ,下面要证
,下面要证![]() ,设
,设![]() ,由导数求出它的最大值,只要最大值小于0,命题即证.
,由导数求出它的最大值,只要最大值小于0,命题即证.
试题解析:(1)![]() 的定义域为
的定义域为![]()
![]()
![]()
当![]() 时
时![]() 所以
所以 ![]() 在
在![]() 递增
递增
当![]() 时
时![]() 所以
所以 ![]() 在
在![]() 递减
递减
(2)由(1)可设![]() 的两个相异实根分别为
的两个相异实根分别为![]() ,
,![]() 满足
满足![]()
且![]() ,
,![]()
由题意可知![]()
又有(1)可知![]() 在
在![]() 递减
递减
故![]()
所以![]()
令![]()
![]()
![]()
令![]()
![]() ,
,
则![]() .
.
当![]() 时,
时,![]() ,
,![]() 是减函数,所以
是减函数,所以![]()
所以当![]() 时,
时,![]() ,即
,即![]()
因为![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,故
,故![]() .
.
综上所述:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分13分)已知椭圆C的中心在坐标原点,离心率
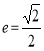 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线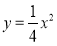 的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点
的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点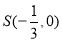 的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】三国魏人刘徽,自撰《海岛算经》,专论测高望远。其中有一题:今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高及去表各几何? 译文如下:要测量海岛上一座山峰
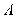 的高度
的高度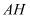 ,立两根高均为
,立两根高均为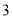 丈的标杆
丈的标杆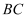 和
和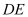 ,前后标杆相距
,前后标杆相距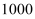 步,使后标杆杆脚
步,使后标杆杆脚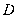 与前标杆杆脚
与前标杆杆脚 与山峰脚
与山峰脚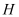 在同一直线上,从前标杆杆脚
在同一直线上,从前标杆杆脚 退行
退行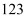 步到
步到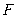 ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,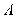 、
、 、
、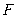 三点共线,从后标杆杆脚
三点共线,从后标杆杆脚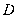 退行
退行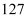 步到
步到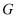 ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,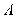 、
、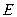 、
、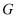 三点也共线,问岛峰的高度
三点也共线,问岛峰的高度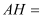 步. (古制:
步. (古制: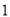 步=
步=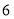 尺,
尺,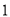 里=
里=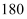 丈=
丈=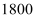 尺=
尺=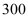 步)
步) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
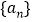 的前
的前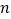 项和为
项和为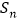 ,且
,且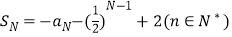 .
.(1)求数列
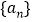 的通项公式,并写出推理过程;
的通项公式,并写出推理过程;(2)令
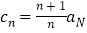 ,
,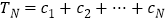 ,试比较
,试比较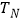 与
与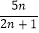 的大小,并给出你的证明.
的大小,并给出你的证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前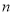 项和为
项和为 ,且
,且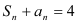 ,
,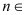 N*
N*(1)求数列
 的通项公式;
的通项公式;(2)已知
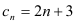 (
(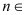 N*),记
N*),记
 (
(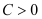 且
且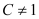 ),是否存在这样的常数
),是否存在这样的常数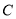 ,使得数列
,使得数列 是常数列,若存在,求出
是常数列,若存在,求出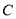 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)若数列
 ,对于任意的正整数
,对于任意的正整数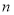 ,均有
,均有 成立,求证:数列
成立,求证:数列 是等差数列.
是等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
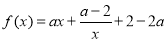
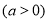 .
.(1)当
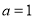 时,求函数
时,求函数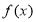 在点
在点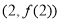 处的切线方程;
处的切线方程;(2)求函数
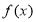 的单调区间;
的单调区间;(3)若
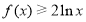 在
在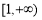 上恒成立,求
上恒成立,求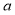 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: (
( )的右焦点为
)的右焦点为 ,且椭圆
,且椭圆 上一点
上一点 到其两焦点
到其两焦点 ,
, 的距离之和为
的距离之和为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)设直线
 :
: (
( )与椭圆
)与椭圆 交于不同两点
交于不同两点 ,
, ,且
,且 ,若点
,若点 满足
满足 ,求
,求 的值.
的值.
相关试题

