【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以 ![]() 为第三项,9为第六项的等比数列公比,则这个三角形是( )
为第三项,9为第六项的等比数列公比,则这个三角形是( )
A.钝角三角形
B.锐角三角形
C.等腰直角三角形
D.以上都不对
参考答案:
【答案】B
【解析】解:∵tanA是以﹣4为第三项,4为第七项的等差数列的公差,
∴tanA=2;
又∵tanB是以 ![]() 为第三项,9为第六项的等比数列的公比.
为第三项,9为第六项的等比数列的公比.
∴tanB=3,
∴ ![]() ,
,
∴可见A,B,C都是锐角,
∴这个三角形是锐角三角形,
故选:B.
【考点精析】利用等差数列的性质和两角和与差的正切公式对题目进行判断即可得到答案,需要熟知在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列;两角和与差的正切公式:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 =lnx+ax2+(2a+1)x.
=lnx+ax2+(2a+1)x.(1)讨论
 的单调性;
的单调性;(2)当a﹤0时,证明
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为
 (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)
 =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,其中
,其中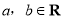 .
.(Ⅰ)若函数
 在
在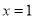 处有极小值
处有极小值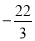 ,求
,求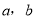 的值;
的值;(Ⅱ)若
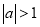 ,设
,设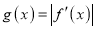 ,求证:当
,求证:当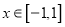 时,
时, 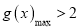 ;
;(Ⅲ)若
 ,对于给定
,对于给定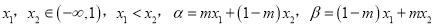 ,其中
,其中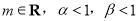 ,若
,若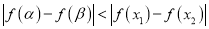 .求
.求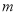 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN.
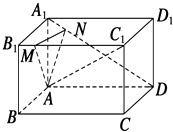
(1)求直线A1D与AM所成角的余弦值;
(2)求直线AD与平面ANM所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
(1)函数y=tanx在定义域内单调递增;
(2)若α,β是锐角△ABC的内角,则sinα>cosβ;
(3)函数y=cos( x+
x+  )的对称轴x=
)的对称轴x=  +kπ,k∈Z;
+kπ,k∈Z;
(4)函数y=sin2x的图象向左平移 个单位,得到y=sin(2x+
个单位,得到y=sin(2x+  )的图象.
)的图象.
其中正确的命题的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S﹣ABCD的底面是正方形,每条侧棱的长都是底面边长的
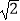 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点. 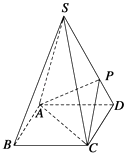
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P﹣AC﹣D的大小.
相关试题

