【题目】如图,四棱锥S﹣ABCD的底面是正方形,每条侧棱的长都是底面边长的 ![]() 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点. 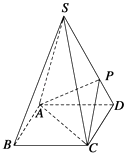
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P﹣AC﹣D的大小.
参考答案:
【答案】
(1)解:连BD,设AC交BD于O,由题意SO⊥AC.
在正方形ABCD中,AC⊥BD,
所以AC⊥平面SBD,得AC⊥SD
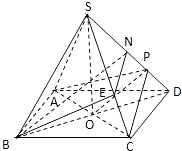
(2)解:设正方形边长a,则SD= ![]() a.
a.
又OD= ![]() a,所以∠SDO=60°,
a,所以∠SDO=60°,
连OP,由(Ⅰ)知AC⊥平面SBD,
所以AC⊥OP,且AC⊥OD,
所以∠POD是二面角P﹣AC﹣D的平面角.
由SD⊥平面PAC,知SD⊥OP,
所以∠POD=30°,
即二面角P﹣AC﹣D的大小为30°
【解析】(1)连BD,设AC交BD于O,则SO⊥AC,在正方形ABCD中,AC⊥BD,根据线面垂直的判定定理可知AC⊥平面SBD,SD平面SBD,根据线面垂直的性质可知AC⊥SD.(2)设正方形边长a,求出SD、OD,得到∠SDO,连OP,根据(Ⅰ)知AC⊥平面SBD,则AC⊥OP,且AC⊥OD,根据二面角平面角的定义可知∠POD是二面角P﹣AC﹣D的平面角,然后在三角形POD求出此角即可.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以
 为第三项,9为第六项的等比数列公比,则这个三角形是( )
为第三项,9为第六项的等比数列公比,则这个三角形是( )
A.钝角三角形
B.锐角三角形
C.等腰直角三角形
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN.
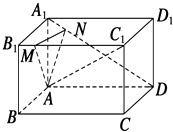
(1)求直线A1D与AM所成角的余弦值;
(2)求直线AD与平面ANM所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
(1)函数y=tanx在定义域内单调递增;
(2)若α,β是锐角△ABC的内角,则sinα>cosβ;
(3)函数y=cos( x+
x+  )的对称轴x=
)的对称轴x=  +kπ,k∈Z;
+kπ,k∈Z;
(4)函数y=sin2x的图象向左平移 个单位,得到y=sin(2x+
个单位,得到y=sin(2x+  )的图象.
)的图象.
其中正确的命题的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设双曲线与椭圆
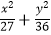 =1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求:
=1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求:
(1)双曲线的标准方程.
(2)若直线L过A(﹣1,2),且与双曲线渐近线y=kx(k>0)垂直,求直线L的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=2x﹣cosx,{an}是公差为
 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5= .
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5= . -
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={x|1≤x≤5},B={x|2≤x≤6},
(1)若x∈A,y∈B且均为整数,求x>y的概率.
(2)若x∈A,y∈B且均为实数,求x>y的概率.
相关试题

