【题目】设函数![]() ,其中
,其中![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处有极小值
处有极小值![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() ,设
,设![]() ,求证:当
,求证:当![]() 时,
时, ![]() ;
;
(Ⅲ)若![]() ,对于给定
,对于给定![]() ,其中
,其中![]() ,若
,若![]() .求
.求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ)证明见解析;(Ⅲ)
;(Ⅱ)证明见解析;(Ⅲ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意得到关于实数![]() 的方程组,求解方程组可得
的方程组,求解方程组可得![]() ;
;
(Ⅱ)首先确定函数取得最值时自变量的位置,然后结合题意进行证明即可得出结论;
(Ⅲ)由题意分类讨论可得![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ) ![]() ,由已知的
,由已知的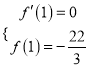 ,
,
解得![]() 或
或![]() .
.
当![]() 时,
时, ![]() 是
是![]() 极小值
极小值
当![]() 时,
时, ![]() 是
是![]() 极大值,故舍去
极大值,故舍去
所以![]()
(Ⅱ) ![]()
因为![]() ,所以函数
,所以函数![]() 的对称轴
的对称轴![]() 位于区间
位于区间![]() 之外,
之外,
于是, ![]() 在
在![]() 上的最大值在两端点处取得,
上的最大值在两端点处取得,
即![]() .
.
于是![]() =
=![]() ≥
≥![]() ,
,
故![]() .
.
(Ⅲ) ![]()
所以,当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
①当![]() 时,
时, ![]() ,
,
![]() ,
,
![]() ,
, ![]()
因为![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
且![]() .
.
因此, ![]() 成立,
成立, ![]() 符合题意.
符合题意.
②当![]() 时,
时, ![]() ,
,
![]() ,
,
于是![]()
所以![]() 成立,
成立, ![]() 不符合题意
不符合题意
③![]() 时,
时, ![]() ,
,
![]() ,
,
![]() .
.
所以![]() 不符合题意.
不符合题意.
综上, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足:a1=1,an+1=
 an+
an+ 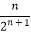
 (n∈N*).
(n∈N*).
(1)求最小的正实数M,使得对任意的n∈N* , 恒有0<an≤M.
(2)求证:对任意的n∈N* , 恒有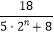 ≤an≤
≤an≤ 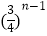 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 =lnx+ax2+(2a+1)x.
=lnx+ax2+(2a+1)x.(1)讨论
 的单调性;
的单调性;(2)当a﹤0时,证明
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为
 (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)
 =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以
 为第三项,9为第六项的等比数列公比,则这个三角形是( )
为第三项,9为第六项的等比数列公比,则这个三角形是( )
A.钝角三角形
B.锐角三角形
C.等腰直角三角形
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN.
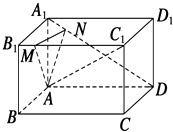
(1)求直线A1D与AM所成角的余弦值;
(2)求直线AD与平面ANM所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
(1)函数y=tanx在定义域内单调递增;
(2)若α,β是锐角△ABC的内角,则sinα>cosβ;
(3)函数y=cos( x+
x+  )的对称轴x=
)的对称轴x=  +kπ,k∈Z;
+kπ,k∈Z;
(4)函数y=sin2x的图象向左平移 个单位,得到y=sin(2x+
个单位,得到y=sin(2x+  )的图象.
)的图象.
其中正确的命题的序号是 .
相关试题

