【题目】给出下列命题:
(1)函数y=tanx在定义域内单调递增;
(2)若α,β是锐角△ABC的内角,则sinα>cosβ;
(3)函数y=cos( ![]() x+
x+ ![]() )的对称轴x=
)的对称轴x= ![]() +kπ,k∈Z;
+kπ,k∈Z;
(4)函数y=sin2x的图象向左平移 ![]() 个单位,得到y=sin(2x+
个单位,得到y=sin(2x+ ![]() )的图象.
)的图象.
其中正确的命题的序号是 .
参考答案:
【答案】(2)
【解析】解:(1)函数y=tanx在每一个区间(kπ﹣ ![]() ,kπ+
,kπ+ ![]() )内单调递增,但在整个定义域内不是单调递增,故(1)错误.(2)若α,β是锐角△ABC的内角,则α+β>
)内单调递增,但在整个定义域内不是单调递增,故(1)错误.(2)若α,β是锐角△ABC的内角,则α+β> ![]() ,即
,即 ![]() >α>
>α> ![]() ﹣β>0,sinα>sin(
﹣β>0,sinα>sin( ![]() ﹣β)=cosβ,故(2)正确.(3)对于函数y=cos(
﹣β)=cosβ,故(2)正确.(3)对于函数y=cos( ![]() x+
x+ ![]() )=cos
)=cos ![]() ,令
,令 ![]() x=kπ,求得x=2kπ,可得函数的图象的对称轴x=2kπ,k∈Z,故(3)错误.(4)函数y=sin2x的图象向左平移
x=kπ,求得x=2kπ,可得函数的图象的对称轴x=2kπ,k∈Z,故(3)错误.(4)函数y=sin2x的图象向左平移 ![]() 个单位,得到y=sin[2(x+
个单位,得到y=sin[2(x+ ![]() )]=sin(2x+
)]=sin(2x+ ![]() )=cos2x 的图象,故(4)错误,
)=cos2x 的图象,故(4)错误,
所以答案是:(2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,其中
,其中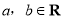 .
.(Ⅰ)若函数
 在
在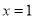 处有极小值
处有极小值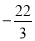 ,求
,求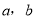 的值;
的值;(Ⅱ)若
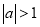 ,设
,设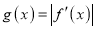 ,求证:当
,求证:当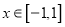 时,
时, 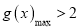 ;
;(Ⅲ)若
 ,对于给定
,对于给定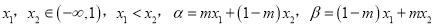 ,其中
,其中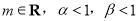 ,若
,若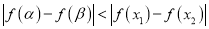 .求
.求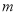 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以
 为第三项,9为第六项的等比数列公比,则这个三角形是( )
为第三项,9为第六项的等比数列公比,则这个三角形是( )
A.钝角三角形
B.锐角三角形
C.等腰直角三角形
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN.
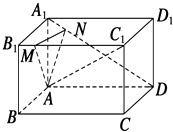
(1)求直线A1D与AM所成角的余弦值;
(2)求直线AD与平面ANM所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S﹣ABCD的底面是正方形,每条侧棱的长都是底面边长的
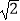 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点. 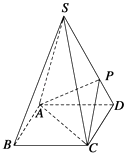
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P﹣AC﹣D的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】设双曲线与椭圆
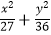 =1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求:
=1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求:
(1)双曲线的标准方程.
(2)若直线L过A(﹣1,2),且与双曲线渐近线y=kx(k>0)垂直,求直线L的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=2x﹣cosx,{an}是公差为
 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5= .
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5= .
相关试题

