【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,右顶点为
,右顶点为![]() ,直线
,直线![]() 过原点
过原点![]() ,且点
,且点![]() 在x轴的上方,直线
在x轴的上方,直线![]() 与
与![]() 分别交直线
分别交直线![]() :
:![]() 于点
于点![]() 、
、![]() .
.
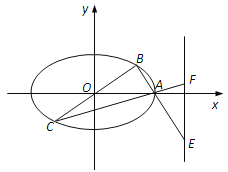
(1)若点![]() ,求椭圆的方程及△ABC的面积;
,求椭圆的方程及△ABC的面积;
(2)若![]() 为动点,设直线
为动点,设直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() 、
、![]() .
.
①试问![]() 是否为定值?若为定值,请求出;否则,请说明理由;
是否为定值?若为定值,请求出;否则,请说明理由;
②求△AEF的面积的最小值.
参考答案:
【答案】(1)![]()
![]() (2)①
(2)①![]() ②
②![]()
【解析】
试题分析:(1)根据题意的离心率及点B的坐标,建立方程,求出a的值,即可求△ABC的面积;(2)①![]() 为定值,证明
为定值,证明![]() ,由(1)得
,由(1)得![]() ,即可得到结论;②设直线AB的方程为y=k1(x-a),直线AC的方程为y=k2(x-a),令x=a+1得,求出△AEF的面积,结合①的结论,利用基本不等式,可求△AEF的面积的最小值
,即可得到结论;②设直线AB的方程为y=k1(x-a),直线AC的方程为y=k2(x-a),令x=a+1得,求出△AEF的面积,结合①的结论,利用基本不等式,可求△AEF的面积的最小值
试题解析:(1)由题意得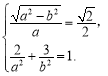 解得
解得![]()
椭圆的方程为![]() ……………………………………………………3分
……………………………………………………3分
△ABC的面积![]() .………………………4分
.………………………4分
(2)① ![]() 为定值,下证之:
为定值,下证之:
证明:设![]() ,则
,则![]() ,且
,且![]() .………………5分
.………………5分
而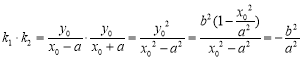 ………………………7分
………………………7分
由离心率![]() ,得
,得![]()
所以![]() ,为定值.……………………………………………8分
,为定值.……………………………………………8分
②由直线的点斜式方程,得直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() . 令
. 令
![]() ,得
,得![]() ,
,![]() .
.
所以,△AEF的面积![]() …………………………10分
…………………………10分
由题意,直线![]() 的斜率
的斜率![]() . 由①,
. 由①,![]()
于是,![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号.………………………………11分
时取等号.………………………………11分
所以,△AEF的面积的最小值为![]() .………12分
.………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 :
: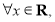
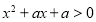 ;
; 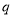 :直线
:直线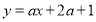 与抛物线
与抛物线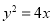 有公共点.如果
有公共点.如果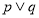 为真命题,
为真命题,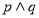 为假命题,求实数
为假命题,求实数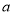 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
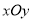 中,直线
中,直线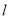 的参数方程为
的参数方程为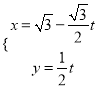 (
(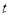 为参数),以原点为极点,
为参数),以原点为极点, 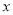 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线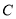 的极坐标方程为
的极坐标方程为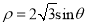 .
.(1)写出曲线
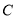 的直角坐标方程;
的直角坐标方程;(2)已知直线
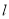 与
与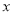 轴的交点为
轴的交点为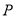 ,与曲线
,与曲线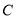 的交点为
的交点为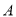 ,
, 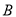 ,若
,若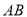 的中点为
的中点为 ,求
,求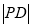 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
, .
.(1)当
 时,求函数
时,求函数 的单调区间及所有零点;
的单调区间及所有零点;(2)设
 ,
, ,
, 为函数
为函数 图象上的三个不同点,且
图象上的三个不同点,且 .问:是否存在实数
.问:是否存在实数 ,使得函数
,使得函数 在点
在点 处的切线与直线
处的切线与直线 平行?若存在,求出所有满足条件的实数
平行?若存在,求出所有满足条件的实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
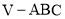 中,平面
中,平面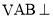 平面
平面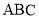 ,
,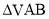 为等边三角形,
为等边三角形,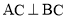 且
且 ,
,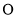 ,
,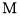 分别为
分别为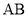 ,
,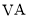 的中点.
的中点.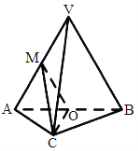
(I)求证:
 平面
平面 ;
;(II)求证:平面
 平面
平面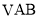 ;
;(III)求三棱锥
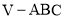 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
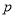 :
: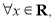
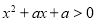 ;
; 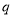 :关于
:关于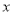 的方程
的方程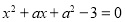 的两根之差的绝对值大于3.如果
的两根之差的绝对值大于3.如果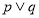 为真命题,
为真命题,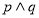 为假命题,求实数
为假命题,求实数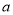 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=(1,2),b=(-2,n),a与b的夹角是45°.
(1) 求b;
(2) 若c与b同向,且a与c-a垂直,求向量c的坐标.
相关试题

