【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为等边三角形,
为等边三角形,
![]() 且
且![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
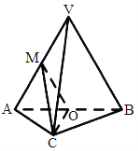
(I)求证:![]() 平面
平面![]() ;
;
(II)求证:平面![]() 平面
平面![]() ;
;
(III)求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】(I)详见解析(II)详见解析(III)![]()
【解析】
试题分析:(Ⅰ)利用三角形的中位线得出OM∥VB,利用线面平行的判定定理证明VB∥平面MOC;(Ⅱ)证明OC⊥平面VAB,即可证明平面MOC⊥平面VAB;(Ⅲ)利用等体积法求三棱锥A-MOC的体积即可
试题解析:(Ⅰ)证明:∵O,M分别为AB,VA的中点,
∴OM∥VB,
∵VB平面MOC,OM平面MOC,
∴VB∥平面MOC;
(Ⅱ)证明:∵AC=BC,O为AB的中点,
∴OC⊥AB,
又∵平面VAB⊥平面ABC,平面ABC∩平面VAB=AB,且OC平面ABC,
∴OC⊥平面VAB,
∵OC平面MOC,
∴平面MOC⊥平面VAB
(Ⅲ)在等腰直角三角形![]() 中,
中,![]() ,
,
所以![]() .
.
所以等边三角形![]() 的面积
的面积![]() .
.
又因为![]() 平面
平面![]() ,
,
所以三棱锥![]() 的体积等于
的体积等于![]() .
.
又因为三棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积相等,
的体积相等,
所以三棱锥![]() 的体积为
的体积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
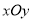 中,直线
中,直线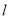 的参数方程为
的参数方程为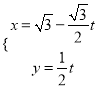 (
(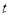 为参数),以原点为极点,
为参数),以原点为极点, 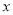 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线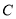 的极坐标方程为
的极坐标方程为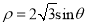 .
.(1)写出曲线
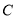 的直角坐标方程;
的直角坐标方程;(2)已知直线
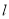 与
与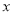 轴的交点为
轴的交点为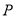 ,与曲线
,与曲线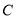 的交点为
的交点为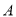 ,
, 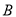 ,若
,若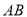 的中点为
的中点为 ,求
,求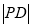 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
, .
.(1)当
 时,求函数
时,求函数 的单调区间及所有零点;
的单调区间及所有零点;(2)设
 ,
, ,
, 为函数
为函数 图象上的三个不同点,且
图象上的三个不同点,且 .问:是否存在实数
.问:是否存在实数 ,使得函数
,使得函数 在点
在点 处的切线与直线
处的切线与直线 平行?若存在,求出所有满足条件的实数
平行?若存在,求出所有满足条件的实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
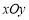 中,椭圆
中,椭圆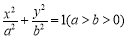 的离心率为
的离心率为 ,右顶点为
,右顶点为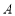 ,直线
,直线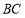 过原点
过原点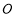 ,且点
,且点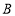 在x轴的上方,直线
在x轴的上方,直线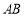 与
与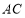 分别交直线
分别交直线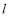 :
: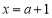 于点
于点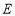 、
、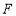 .
.
(1)若点
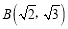 ,求椭圆的方程及△ABC的面积;
,求椭圆的方程及△ABC的面积;(2)若
 为动点,设直线
为动点,设直线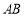 与
与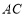 的斜率分别为
的斜率分别为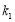 、
、 .
.①试问
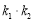 是否为定值?若为定值,请求出;否则,请说明理由;
是否为定值?若为定值,请求出;否则,请说明理由;②求△AEF的面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
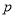 :
: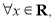
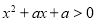 ;
; 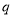 :关于
:关于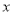 的方程
的方程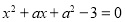 的两根之差的绝对值大于3.如果
的两根之差的绝对值大于3.如果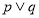 为真命题,
为真命题,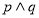 为假命题,求实数
为假命题,求实数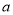 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=(1,2),b=(-2,n),a与b的夹角是45°.
(1) 求b;
(2) 若c与b同向,且a与c-a垂直,求向量c的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
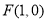 ,直线
,直线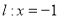 ,动点
,动点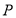 到点
到点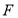 的距离等于它到直线
的距离等于它到直线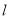 的距离.
的距离.(Ⅰ)求点
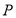 的轨迹
的轨迹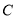 的方程;
的方程;(Ⅱ)是否存在过
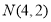 的直线
的直线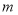 ,使得直线
,使得直线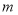 被曲线
被曲线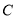 截得的弦
截得的弦 恰好被点
恰好被点 所平分?
所平分?
相关试题

