【题目】定义在R上的函数f(x)=ax2+x.
(Ⅰ)当a>0时,求证:对任意的x1,x2∈R都有![]() [f(x1)+f(x2)]
[f(x1)+f(x2)]![]() 成立;
成立;
(Ⅱ)当x∈[0,2]时,|f(x)|≤1恒成立,求实数a的取值范围;
(Ⅲ)若a=![]() ,点p(m,n2)(m∈Z,n∈Z)是函数y=f(x)图象上的点,求m,n.
,点p(m,n2)(m∈Z,n∈Z)是函数y=f(x)图象上的点,求m,n.
参考答案:
【答案】(Ⅰ)详见解析(II)-![]() ≤a≤-
≤a≤-![]() (Ⅲ)m=n=0或者m=-4,n=0
(Ⅲ)m=n=0或者m=-4,n=0
【解析】
(Ⅰ)作差比较;
(Ⅱ)分离变量后再将恒成立转化为最值;
(Ⅲ)根据两个整数的和与积都为偶数,得这两个整数均为偶数.
解:(Ⅰ)证明:∵![]() [f(x1)+f(x2)]-f(
[f(x1)+f(x2)]-f(![]() )
)
=![]() (ax12+x1+ax22+x2)-a(
(ax12+x1+ax22+x2)-a(![]() )2-
)2-![]()
=![]() ,
,
∵a>0,∴![]() [f(x1)+f(x2)]-f(
[f(x1)+f(x2)]-f(![]() )≥0,
)≥0,
∴![]() [f(x1)+f(x2)]≥f(
[f(x1)+f(x2)]≥f(![]() ).
).
(Ⅱ)当x=0时,|f(x)|≤1显然成立,此时a∈R;
当x∈(0,2]时,|f(x)|≤1-1≤ax2+x≤1![]() ≤a≤
≤a≤![]()
-(![]() )2-
)2-![]() ≤a≤(
≤a≤(![]() )2-
)2-![]() 恒成立,
恒成立,
∵x∈(0,2],∴-(![]() )2-
)2-![]() 有最大值-
有最大值-![]() ,(
,(![]() )2-
)2-![]() 有最小值-
有最小值-![]() ,
,
∴-![]() ≤a≤-
≤a≤-![]() .
.
(Ⅲ)∵a=![]() ,∴f(x)=
,∴f(x)=![]() x2+x,
x2+x,
∵P(m,n2)在函数f(x)的图象上,∴![]() m2+m=n2,
m2+m=n2,
变形得(m+2)2-4n2=4,
∴(m+2-2n)(m+2+2n)=4,且m∈Z,n∈Z,
∵(m+2-2n)+(m+2+2n)=2m+4为偶数,
∴m+2-2n与m+2+2n同为偶数,
∴![]() 或
或![]()
解得:![]() 或
或![]()
故答案为:m=n=0或者m=-4,n=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,角
,角 的终边经过点
的终边经过点 .若
.若 是
是 的图象上任意两点,且当
的图象上任意两点,且当 时,
时, 的最小值为
的最小值为 .
.(1)求
 或
或 的值;
的值;(2)求函数
 在
在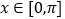 上的单调递减区间;
上的单调递减区间;(3)当
 时,不等式
时,不等式 恒成立,求
恒成立,求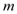 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log4(22x+1)+mx的图象经过点
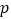
 .
.(Ⅰ)求m值并判断的奇偶性;
(Ⅱ)设g(x)=log4(2x+x+a)f(x),若关于x的方程f(x)=g(x)在x∈[-2,2]上有且只有一个解,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区某农产品近几年的产量统计如下表:

(1)根据表中数据,建立
 关于
关于 的线性回归方程
的线性回归方程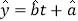 ;
;(2)若近几年该农产品每千克的价格
 (单位:元)与年产量
(单位:元)与年产量 满足的函数关系式为
满足的函数关系式为 ,且每年该农产品都能售完.
,且每年该农产品都能售完.①根据(1)中所建立的回归方程预测该地区
 年该农产品的产量;
年该农产品的产量;②当
 为何值时,销售额
为何值时,销售额 最大?
最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了比较注射
 ,
, 两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物 ,另一组注射药物
,另一组注射药物 .表1和表2分别是注射药物
.表1和表2分别是注射药物 和
和 后的试验结果.(疱疹面积单位:
后的试验结果.(疱疹面积单位: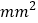 )
)表1:注射药物
 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
表2:注射药物
 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;


(2)完成下面
 列联表,并回答能否有
列联表,并回答能否有 的把握认为“注射药物
的把握认为“注射药物 后的疱疹面积与注射药物
后的疱疹面积与注射药物 后的疱疹面积有差异”.
后的疱疹面积有差异”.表3:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,其中c为常数,且函数f(x)的图象过原点.
,其中c为常数,且函数f(x)的图象过原点.(1)求c的值,并求证:f(
 )+f(x)=1;
)+f(x)=1;(2)判断函数f(x)在(-1,+∞)上的单调性,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x>
 时,f(x+
时,f(x+  )=f(x﹣
)=f(x﹣  ).则f(6)=( )
).则f(6)=( )
A.﹣2
B.﹣1
C.0
D.2
相关试题

