【题目】以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经X表示。
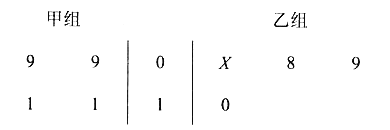
(1)如果X=8,求乙组同学植树棵数的平均数和方差
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率
参考答案:
【答案】(1)10,1;(2)![]() .
.
【解析】
茎叶图中间表示十位,两边表示个位,当x=8,表示出甲乙的植树棵数,求解;
甲、乙两组中随机选取一名同学需将甲乙的各种情况表示出来,排列出所有情况,(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A2,B2),(A3,B3),(A1,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),其中满足条件的共4个,古典概型,求解。
解(Ⅰ)当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,
所以平均数为
![]()
方差为
![]()
(Ⅱ)记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,11;乙组四名同学为B1,B2,B3,B4,他们植树的棵数依次为9,8,9,10,分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,它们是:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A2,B2),(A3,B3),(A1,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结果有4个,它们是:(A1,B4),(A2,B4),(A3,B2),(A4,B2),故所求概率为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
 (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过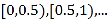 的部分按平价收费,超出
的部分按平价收费,超出 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准
 (吨),估计
(吨),估计 的值,并说明理由.
的值,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图.

记
 表示
表示 台机器在三年使用期内需更换的易损零件数,
台机器在三年使用期内需更换的易损零件数, 表示
表示 台机器在购买易损零件上所需的费用(单位:元),
台机器在购买易损零件上所需的费用(单位:元), 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.(1)若
 ,求
,求 与
与 的函数解析式;
的函数解析式;(2)若要求 “需更换的易损零件数不大于
 ”的频率不小于
”的频率不小于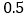 ,求
,求 的最小值;
的最小值; (3)假设这
 台机器在购机的同时每台都购买
台机器在购机的同时每台都购买 个易损零件,或每台都购买
个易损零件,或每台都购买 个易损零件,分别计算这
个易损零件,分别计算这 台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买
台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买 台机器的同时应购买
台机器的同时应购买 个还是
个还是 个易损零件?
个易损零件? -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 (
( )的右焦点为
)的右焦点为 ,右顶点为
,右顶点为 ,已知
,已知 ,其中
,其中 为原点,
为原点, 为椭圆的离心率.
为椭圆的离心率.(Ⅰ)求椭圆的方程;
(Ⅱ)设过点
 的直线
的直线 与椭圆交于点
与椭圆交于点 (
( 不在
不在 轴上),垂直于
轴上),垂直于 的直线与
的直线与 交于点
交于点 ,与
,与 轴交于点
轴交于点 ,若
,若 ,且
,且 ,求直线的
,求直线的 斜率.
斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市
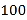 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以 ,
, ,
,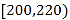 ,
, ,
, ,
, ,
, 分组的频率分布直方图如图.
分组的频率分布直方图如图.
(1)求直方图中
 的值;
的值;(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为
 ,
, ,
, ,
, 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在
户居民,则月平均用电量在 的用户中应抽取多少户?
的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的各项均为正整数,其前n项和为Sn , an+1=
 ,若S3=10,则S180=( )
,若S3=10,则S180=( )
A.600或900
B.900或560
C.900
D.600 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在区间D上的函数f(x)和g(x),如果对任意x∈D,都有|f(x)﹣g(x)|≤1成立,则称f(x)在区间D上可被g(x)替代,D称为“替代区间”.给出以下问题:
①f(x)=x2+1在区间(﹣∞,+∞)上可被g(x)=x2+ 替代;
替代;
②如果f(x)=lnx在区间[1,e]可被g(x)=x﹣b替代,则﹣2≤b≤2;
③设f(x)=lg(ax2+x)(x∈D1),g(x)=sinx(x∈D1),则存在实数a(a≠0)及区间D1 , D2 , 使得f(x)在区间D1∩D2上被g(x)替代.
其中真命题是( )
A.①②③
B.②③
C.①
D.①②
相关试题

