【题目】已知函数f(x)=x3-3ax+e,g(x)=1-lnx,其中e为自然对数的底数.
(I)若曲线y=f(x)在点(1,f(1))处的切线与直线l:x+2y=0垂直,求实数a的值;
(II)设函数F(x)=-x[g(x)+![]() x-2],若F(x)在区间(m,m+1)(m∈Z)内存在唯一的极值点,求m的值;
x-2],若F(x)在区间(m,m+1)(m∈Z)内存在唯一的极值点,求m的值;
(III)用max{m,n}表示m,n中的较大者,记函数h(x)=max{f(x),g(x)}(x>0). 若函数h(x)在(0,+∞)上恰有2个零点,求实数a的取值范围.
参考答案:
【答案】(I)a=![]() ; (II)m=0或m=3; (III)a>
; (II)m=0或m=3; (III)a>![]() .
.
【解析】试题分析:(Ⅰ)求出函数的导数,计算f′(1),求出a的值即可;
(Ⅱ)求出函数F(x)的导数,根据函数的单调性求出函数的极值点,求出对应的m的值即可;
(Ⅲ)通过讨论a的范围求出函数f(x)的单调区间,结合函数的单调性以及函数的零点个数确定a的范围即可.
试题解析:
(I)易得,f '(x)=3x2-3a,所以f '(1)=3-3a,
依题意,(3-3a)(-![]() )=-1,解得a=
)=-1,解得a=![]() ;
;
(II)因为F(x)=-x[g(x)+![]() x-2]=-x[(1-lnx)+
x-2]=-x[(1-lnx)+![]() x-2]=xlnx-
x-2]=xlnx-![]() x2+x,
x2+x,
则F' (x)=lnx+l-x+l=lnx-x+2. 设t(x)=lnx-x+2,
则t '(x)=![]() -1=
-1=![]() .
.
令t '(x)=0,得x=1.
则由t '(x)>0,得0<x<1,F '(x)为增函数;
由t '(x)<0,得x>1,F '(x)为减函数;
而F '(![]() )=-2-
)=-2-![]() +2=-
+2=-![]() <0,F '(1)=1>0.
<0,F '(1)=1>0.
则F '(x)在(0,1)上有且只有一个零点x1,
且在(0,x1)上F '(x)<0,F(x)为减函数;
在(x1,1)上F '(x)>0,F(x)为增函数.
所以x1为极值点,此时m=0.
又F '(3)=ln3-1>0,F '(4)=21n2-2<0,
则F '(x)在(3,4)上有且只有一个零点x2,
且在(3,x2)上F '(x)>0,F(x)为增函数;
在(x2,4)上F '(x)<0,F(x)为减函数.
所以x2为极值点,此时m=3.
综上m=0或m=3.
(III)(1)当x∈(0,e)时,g(x)>0,依题意,h(x)≥g(x)>0,不满足条件;
(2)当x=e时,g(e)=0,f(e)=e3-3ae+e,
①若f(e)=e3-3ae+e≤0,即a≥![]() ,则e是h(x)的一个零点;
,则e是h(x)的一个零点;
②若f(e)=e3-3ae+e>0,即a<![]() ,则e不是h(x)的零点;
,则e不是h(x)的零点;
(3)当x∈(e,+∞)时,g(x)<0,所以此时只需考虑函数f(x)在(e,+∞)上零点的情况.
因为f '(x)=3x2-3a>3e2-3a,所以
①当a≤e2时,f '(x)>0,f(x)在(e,+∞)上单调递增.
又f(e)=e3-3ae+e,所以
(i)当a≤![]() 时,f(e)≥0,f(x)在(e,+∞)上无零点;
时,f(e)≥0,f(x)在(e,+∞)上无零点;
(ii)当![]() <a≤e2时,f(e)<0,
<a≤e2时,f(e)<0,
又f(2e)=8e3-6ae+e≥8e3-6e3+e>0,
所以此时f(x)在(e,+∞)上恰有一个零点;
②当a>e2时,令f '(x)=0,得x=±![]() .
.
由f '(x)<0,得e<x<![]() ;
;
由f '(x)>0,得x>![]() ;
;
所以f(x)在(e, ![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
因为f(e)=e3-3ae+e<e3-3e3+e<0,
f(2a)=8a3-6a2+e>8a2-6a2+e=2a2+e>0,
所以此时f(x)在(e,+∞)上恰有一个零点;
综上,a>![]() .
.
-
科目: 来源: 题型:
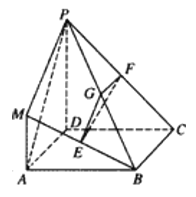
查看答案和解析>>【题目】在如图所示的几何体中,四边形
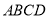 是正方形,
是正方形, 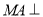 平面
平面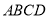 ,
, 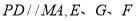 分别为
分别为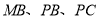 的中点,且
的中点,且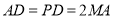 .
.
(1)求证:平面
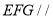 平面
平面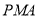 ;
;(2)求证:平面
 平面
平面 ;
;(3)求三棱锥
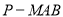 与四棱锥
与四棱锥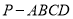 的体积之比.
的体积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数
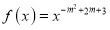 (m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.(1)求函数f(x)的解析式;
(2)设函数
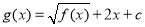 ,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围.
,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①集合
 的子集个数有16个;②定义在
的子集个数有16个;②定义在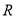 上的奇函数
上的奇函数 必满足
必满足 ;③
;③ 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与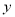 轴相交;⑤
轴相交;⑤ 在
在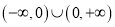 上是减函数。
上是减函数。其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司对新研发的一种产品进行试销,得到如下数据及散点图:

其中
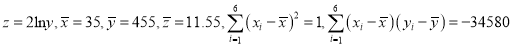 ,
, 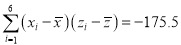 ,
, 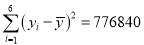 ,
, 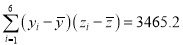 .
.(1)根据散点图判断
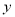 与
与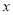 ,
,  与
与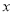 哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?(2)根据(1)的判断结果及数据,建立
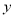 关于
关于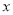 的回归方程(运算过程及回归方程中的系数均保留两位有效数字).
的回归方程(运算过程及回归方程中的系数均保留两位有效数字).(3)定价为150元/
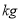 时,天销售额的预报值为多少元?
时,天销售额的预报值为多少元?附:对于一组数据
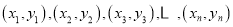 ,其回归直线
,其回归直线 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为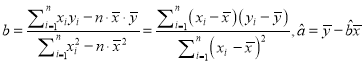
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区工商局、消费者协会在
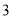 月
月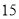 号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取
号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取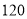 名群众,按他们的年龄分组:第
名群众,按他们的年龄分组:第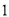 组
组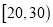 ,第
,第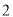 组
组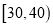 ,第
,第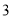 组
组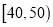 ,第
,第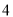 组
组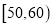 ,第
,第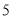 组
组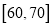 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.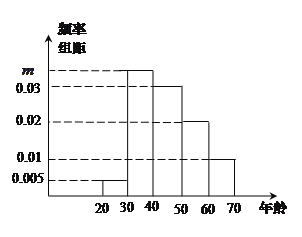
(Ⅰ)若电视台记者要从抽取的群众中选
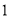 人进行采访,求被采访人恰好在第
人进行采访,求被采访人恰好在第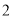 组或第
组或第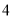 组的概率;
组的概率;(Ⅱ)已知第
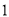 组群众中男性有
组群众中男性有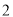 人,组织方要从第
人,组织方要从第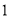 组中随机抽取
组中随机抽取 名群众组成维权志愿者服务队,求至少有两名女性的概率.
名群众组成维权志愿者服务队,求至少有两名女性的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 为矩形,
为矩形,  平面
平面 ,
,  ,点
,点 为
为 的中点,点
的中点,点 在棱
在棱 上移动.
上移动.(1)当点
 为
为 的中点时,试判断
的中点时,试判断 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;(2)求证:无论点
 在
在 的何处,都有
的何处,都有 ;
;(3)求二面角
 的余弦值.
的余弦值.
相关试题

