【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为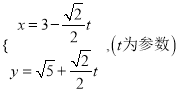 。在以原点
。在以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() 。
。
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点P坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值。
的值。
参考答案:
【答案】(1)![]()
![]() (2)
(2)![]()
【解答】解:(Ⅰ)由 得直线l的普通方程为x+y﹣3﹣
得直线l的普通方程为x+y﹣3﹣![]() =0
=0
又由![]() 得 ρ2=2
得 ρ2=2![]() ρsinθ,化为直角坐标方程为x2+(y﹣
ρsinθ,化为直角坐标方程为x2+(y﹣![]() )2=5;
)2=5;
(Ⅱ)把直线l的参数方程代入圆C的直角坐标方程,
得(3﹣![]() t)2+(
t)2+(![]() t)2=5,即t2﹣3
t)2=5,即t2﹣3![]() t+4=0
t+4=0
设t1,t2是上述方程的两实数根,
所以t1+t2=3![]()
又直线l过点P![]() ,A、B两点对应的参数分别为t1,t2,
,A、B两点对应的参数分别为t1,t2,
所以|PA|+|PB|=|t1|+|t2|=t1+t2=3![]() .
.
【解析】试题分析:(1)由加减消元得直线![]() 的普通方程,由
的普通方程,由![]() 得圆
得圆![]() 的直角坐标方程;(2)把直线l的参数方程代入圆C的直角坐标方程,由直线参数方程几何意义得|PA|+|PB|=|t1|+|t2|=t1+t2,再根据韦达定理可得结果
的直角坐标方程;(2)把直线l的参数方程代入圆C的直角坐标方程,由直线参数方程几何意义得|PA|+|PB|=|t1|+|t2|=t1+t2,再根据韦达定理可得结果
试题解析:解:(Ⅰ)由 得直线l的普通方程为x+y﹣3﹣
得直线l的普通方程为x+y﹣3﹣![]() =0
=0
又由![]() 得 ρ2=2
得 ρ2=2![]() ρsinθ,化为直角坐标方程为x2+(y﹣
ρsinθ,化为直角坐标方程为x2+(y﹣![]() )2=5;
)2=5;
(Ⅱ)把直线l的参数方程代入圆C的直角坐标方程,
得(3﹣![]() t)2+(
t)2+(![]() t)2=5,即t2﹣3
t)2=5,即t2﹣3![]() t+4=0
t+4=0
设t1,t2是上述方程的两实数根,
所以t1+t2=3![]()
又直线l过点P![]() ,A、B两点对应的参数分别为t1,t2,
,A、B两点对应的参数分别为t1,t2,
所以|PA|+|PB|=|t1|+|t2|=t1+t2=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,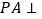 平面
平面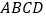 ,底面
,底面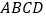 为菱形,且
为菱形,且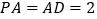 ,
,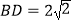 ,
, 、
、 分别为
分别为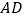 、
、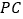 中点.
中点.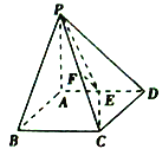
(1)求点
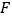 到平面
到平面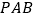 的距离;
的距离;(2)求证:平面
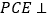 平面
平面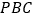 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案
不善于使用学案
总计
学习成绩优秀
40
学习成绩一般
30
总计
100
参考公式:
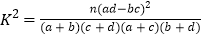 ,其中
,其中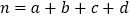 .
.参考数据:
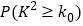
0.050
0.010
0.001
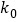
3.841
6.635
10.828
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)若从学习成绩优秀的同学中随机抽取10人继续调查,采用何种方法较为合理,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“菊花”型烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂.通过研究,发现该型烟花爆裂时距地面的高度
 (单位:米)与时间
(单位:米)与时间 (单位:秒)存在函数关系,并得到相关数据如表:
(单位:秒)存在函数关系,并得到相关数据如表:时间

1


高度




(1)根据表中数据,从下列函数中选取一个函数描述该型烟花爆裂时距地面的高度
 与时间
与时间 的变化关系:
的变化关系:  ,
,  ,
,  ,确定此函数解析式并简单说明理由;
,确定此函数解析式并简单说明理由;(2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求此时烟花距地面的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 ,解不等式
,解不等式 ;
;(2)若存在实数
 ,使得不等式
,使得不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016~2017·郑州高一检测)过点M(1,2)的直线l与圆C:(x-3)2+(y-4)2=25交于A,B两点,C为圆心,当∠ACB最小时,直线l的方程是 ( )
A. x-2y+3=0 B. 2x+y-4=0
C. x-y+1=0 D. x+y-3=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
甲
82
82
79
95
87
乙
95
75
80
90
85
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
相关试题

